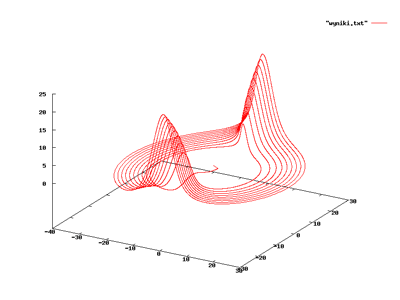
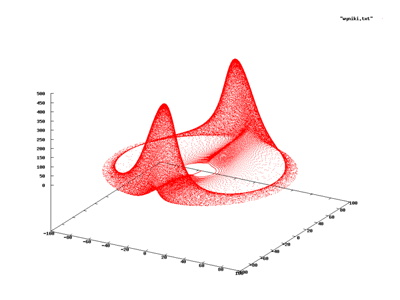
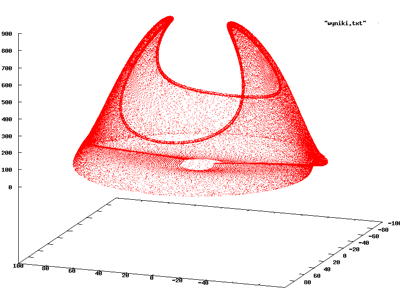
The Rabinovich-Fabrikant equations are a set of three coupled ordinary differential equations exhibiting chaotic behavior for certain values of the parameters. The equations are:
An example of chaotic behavior is obtained for γ = 0.87 and α = 1.1. The correlation dimension was found to be 2.19 ± 0.01. (See Grassberger et al. 1983).
Images: Jacek Tyburczyk See also * List of chaotic maps Links * Weisstein, Eric W. "Rabinovich-Fabrikant Equation." From MathWorld--A Wolfram Web Resource. References * P. Grassberger and I. Procaccia (1983). "Measuring the strangeness of strange attractors". Physica D 9: 189-208. (LINK) * Rabinovich, M. I. and Fabrikant, A. L. (1979). "Stochastic Self-Modulation of Waves in Nonequilibrium Media". Sov. Phys. JETP 50: 311. Retrieved from "http://en.wikipedia.org/"
|
|