Geometric mean

The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, which is what most people think of with the word "average," except that instead of adding the set of numbers and then dividing the sum by the count of numbers in the set, n, the numbers are multiplied and then the nth root of the resulting product is taken.

For instance, the geometric mean of two numbers, say 2 and 8, is just the square root (i.e., the second root) of their product, 16, which is 4. As another example, the geometric mean of 1, ½, and ¼ is the cube root (i.e., the third root) of their product, 0.125, which is ½.

The geometric mean can be understood in terms of geometry. The geometric mean of two numbers, a and b, is simply the side length of the square whose area is equal to that of a rectangle with side lengths a and b. That is, what is n such that n² = a × b? Similarly, the geometric mean of three numbers, a, b, and c, is the side length of a cube whose volume is the same as that of a rectangular prism with side lengths equal to the three given numbers. This geometric interpretation of the mean is very likely what gave it its name.

The geometric mean only applies to positive numbers.[1] It is also often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature, such as data on the growth of the human population or interest rates of a financial investment. The geometric mean is also one of the three classic Pythagorean means, together with the aforementioned arithmetic mean and the harmonic mean.

Calculation

The geometric mean of a data set [a₁, a₂, ..., a_n] is given by

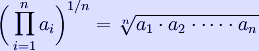The geometric mean of a data set is smaller than or equal to the data set's arithmetic mean (the two means are equal if and only if all members of the data set are equal). This allows the definition of the arithmetic-geometric mean, a mixture of the two which always lies in between.

The geometric mean is also the arithmetic-harmonic mean in the sense that if two sequences (an) and (hn) are defined:

and

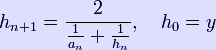
then an and hn will converge to the geometric mean of x and y.

Relationship with arithmetic mean of logarithms

By using logarithmic identities to transform the formula, we can express the multiplications as a sum and the power as a multiplication.

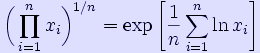
This is sometimes called the log-average. It is simply computing the arithmetic mean of the logarithm transformed values of xi (i.e. the arithmetic mean on the log scale) and then using the exponentiation to return the computation to the original scale. I.e., it is the generalised f-mean with f(x) = ln x.

Therefore the geometric mean is related to the log-normal distribution. The log-normal distribution is a distribution which is normal for the logarithm transformed values. We see that the geometric mean is the exponentiated value of the arithmetic mean of the log transformed values, i.e. e^mean(ln(X)).

Notes and references

1. ^ The geometric mean only applies to positive numbers in order to avoid taking the root of a negative product, which would result in imaginary numbers, and also to satisfy certain properties about means, which is explained later in the article.