Fransén–Robinson constant

The Fransén–Robinson constant, sometimes denoted F, is the mathematical constant that represents the area between the graph of the reciprocal Gamma function, 1 / Γ(x), and the positive x axis. That is,

The Fransén–Robinson constant has numerical value F = 2.8077702420285... (sequence A058655 in OEIS), with the continued fraction representation [2; 1, 4, 4, 1, 18, 5, 1, 3, 4, 1, 5, 3, 6, ...] (sequence A046943 in OEIS). Its proximity to Euler's number e = 2.71828... follows from the fact that the integral can be approximated by the sum

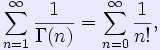
the standard series for e. The difference is given by

and also by

The Fransén–Robinson constant can also be expressed using the Mittag-Leffler function as the limit

It is however unknown whether F can be expressed in closed form in terms of other known constants.

A fair amount of effort has been made to calculate the numerical value of the Fransén–Robinson constant with high accuracy. The value was computed to 36 decimal places by H. P. Robinson using 11-point Newton–Cotes quadrature, with 65 digits by A. Fransén using Euler–Maclaurin summation, and with 80 digits by Fransén and S. Wrigge using Taylor series and other methods. William A. Johnson computed 300 digits, and Pascal Sebah was able to compute 600 digits using Clenshaw–Curtis integration.

References

* Steve Finch, Fransén–Robinson Constant
* Weisstein, Eric W., "Fransén–Robinson Constant" from MathWorld.
* Borwein, Jonathan; David Bailey, Roland Girgensohn (2003). Experimentation in Mathematics – Computational Paths to Discovery. A K Peters. p. 288. ISBN 1-56881-136-5.
* The value of the Fransén–Robinson constant to 300 decimal places