Watt's curve

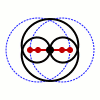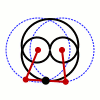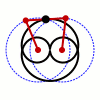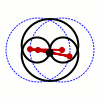
In mathematics, Watt's curve is a plane algebraic curve of degree six. It is generated by two circles of radius r with centers a distance d apart. A line segment of length ℓ attaches to a point on each of the circles, and the midpoint of the line segment traces out the Watt curve as the circles rotate. It arose in connection with James Watt's pioneering work on the steam engine.

The equation of the curve can be given as

((x² + y²)² + 4y² − a²(x² + y²))(x² + y² − a²) =

(b² − 1)(x² + y²)(2a² + 1 − 2(x² + y²) − b²).

Here a = d²/4r² and b = ℓ²/d².

The Watt curve is a curve of genus one, with j-invariant