Newton fractal for three degree-3 roots (p(z) = z3 − 1), coloured by number of iterations required (*) The Newton fractal is a boundary set in the complex plane which is characterized by Newton's method applied to a fixed polynomial Many points of the complex plane are associated with one of the To plot interesting pictures, one may first choose a specified number d of complex points (ζ1,...,ζd) and compute the coëfficients (p1,...,pd) of the polynomial Then for a rectangular lattice zmn = z00 + mΔx + inΔy, m = 0, ..., M - 1, n = 0, ..., N - 1 of points in References * J. H. Hubbard, D. Schleicher, S. Sutherland: How to Find All Roots of Complex Polynomials by Newton's Method, Inventiones Mathematicae vol. 146 (2001) – with a discussion of the global structure of Newton fractals * On the Number of Iterations for Newton's Method by Dierk Schleicher July 21, 2000 * Newton's Method as a Dynamical System by Johannes Rueckert Retrieved from "http://en.wikipedia.org/" |
|
. When there are no attractive cycles, it divides the complex plane into regions Gk, each of which is associated with a root ζk of the polynomial, 
. In this way the Newton fractal is similar to the Mandelbrot set, and like other fractals it exhibits a complex appearance arising from a simple description. It is relevant to numerical analysis because it shows that (outside the region of quadratic convergence) the Newton method can be very sensitive to its choice of start point.
roots of the polynomial in the following way: the point is used as starting value z0 for Newton's iteration 
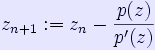, yielding a sequence of points z1, z2, .... If the sequence converges to the root ζk, then z0 was an element of the region Gk. However, for every polynomial of degree at least 2 there are points for which the Newton iteration does not converge to any root: examples are the boundaries of the basins of attraction of the various roots. There are even polynomials for which open sets of starting points fail to converge to any root: a simple example is z3-2z+2, where some points are attracted by the cycle 0, 1, 0, 1 ... rather than by a root.
.
, one finds the index k(m,n) of the corresponding root ζk(m,n) and uses this to fill an M×N raster grid by assigning to each point (m,n) a colour fk(m,n). Additionally or alternatively the colours may be dependent on the distance D(m,n), which is defined to be the first value D such that |zD - ζk(m,n)| < ε for some previously fixed small ε > 0.
