An apeirogon is a degenerate polygon with a countably infinite number of sides. It is the limit of a sequence of polygons with more and more sides.

Like any polygon, it is a sequence of line segments (edges) and angles (corners). But whereas an ordinary polygon has no ends because it is a closed circuit, an apeirogon can also have no ends because you can never make the infinite number of steps needed to get to the end in either direction. Closed apeirogons also exist. They occur when the corners form sequences (one in each direction, starting from any point) whose limits converge on the same point. Such a point is called an accumulation point, and any closed apeirogon must have at least one of them.

Regular apeirogons

A regular apeirogon has equal-length sides and equal corner angles, just like any regular polygon. Its Schläfli symbol is {∞}.

If the corner angles are 180 degrees, the overall form of the apeirogon resembles a circle of infinite radius or a straight line:

Skew forms

For some time, people thought this was the only regular example. Then Branko Grünbaum discovered two more.

If the corner angles alternate either side of the figure, the apeirogon resembles a zig-zag, and has 2*∞ Frieze group symmetry.

If each corner angle is displaced out of the plane of the previous angle, the apeirogon resembles a three-dimensional helix. A polygon such as this which does not lie in a plane, is said to be skew. The sketch on the right is a 3D perspective view of such a regular skew apeirogon.

This polygon can be constructed from a sequential subset of edges within an infinite stack of uniform n-gonal antiprisms, although unlike the antiprisms, the twist angle is not limited to an integer divisor of a complete turn. It has screw axis.

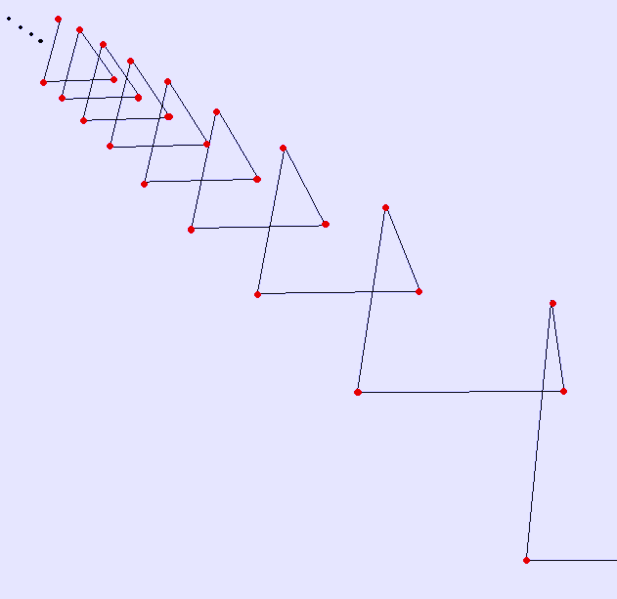
A regular apeirogon as an equilateral triangular helix, drawn in perspective.

See also

* apeirohedron

References

* Coxeter, H. S. M. (1973). Regular Polytopes, 3rd ed., New York: Dover Publications, 121–122. ISBN 0-486-61480-8. p.296, Table II: Regular honeycombs

* Grünbaum, B. Regular polyhedra - old and new, Aequationes Math. 16 (1977) p.1-20

* Peter McMullen, Egon Schulte, Abstract Regular Polytopes, Cambridge University Press, 2002. ISBN 0-521-81496-0 (Page 25)

Links

* Russell, Robert, Apeirogon at MathWorld.

* Olshevsky, George, Apeirogon at Glossary for Hyperspace.

Equilateral triangular helix (obj)

v 1 0 0
v -0.5 0.866 1
v -0.5 -0.866 2
v 1 0 3
v -0.5 0.866 4
v -0.5 -0.866 5
v 1 0 6
v -0.5 0.866 7
v -0.5 -0.866 8
v 1 0 9
v -0.5 0.866 10
v -0.5 -0.866 11
v 1 0 12
v -0.5 0.866 13
v -0.5 -0.866 14
v 1 0 15
v -0.5 0.866 16
v -0.5 -0.866 17
v 1 0 18
v -0.5 0.866 19
v -0.5 -0.866 20
v 1 0 21
v -0.5 0.866 22
v -0.5 -0.866 23
v 1 0 24
v -0.5 0.866 25
v -0.5 -0.866 26
v 1 0 27
v -0.5 0.866 28
v -0.5 -0.866 29
l 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29