.
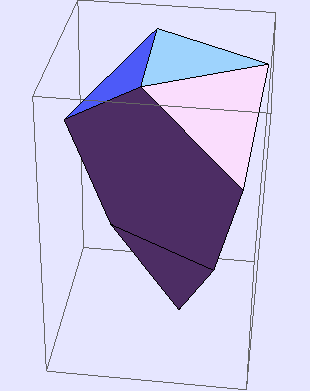
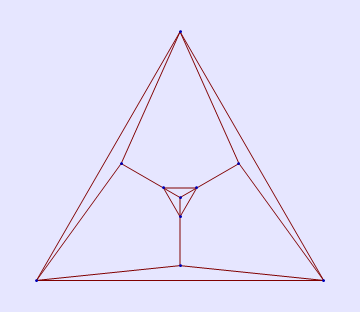
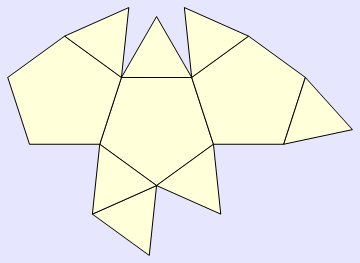
Augmented tridiminished icosahedron
In[62]:=
![]()
Out[62]=
In[63]:=
![]()
Out[63]=
![]()
In[64]:=
![]()
Out[64]=
![]()
In[65]:=
![]()
Out[65]=
![]()
In[66]:=
![]()
Out[66]=
![]()
In[67]:=
![]()
Out[67]=
In[68]:=
![]()
Out[68]=
In[69]:=
![]()
Out[69]=
![]()
In[70]:=
![]()
Out[70]//InputForm=
Graphics3D[GraphicsComplex[{{0, 0, Sqrt[(903 + 350*Sqrt[2] - 223*Sqrt[5] - 282*Sqrt[10])/6]/84 +
Root[9 - 2472*#1^2 + 8752*#1^4 - 8832*#1^6 + 2304*#1^8 & , 1, 0]},
{-(1/Sqrt[3]), 0, Sqrt[(903 + 350*Sqrt[2] - 223*Sqrt[5] - 282*Sqrt[10])/6]/84 +
Root[1 - 84*#1^2 + 144*#1^4 & , 1, 0]}, {-1/(2*Sqrt[3]), -1/2,
Sqrt[(903 + 350*Sqrt[2] - 223*Sqrt[5] - 282*Sqrt[10])/6]/84 +
Root[1 - 84*#1^2 + 144*#1^4 & , 4, 0]}, {-1/(2*Sqrt[3]), 1/2,
Sqrt[(903 + 350*Sqrt[2] - 223*Sqrt[5] - 282*Sqrt[10])/6]/84 +
Root[1 - 84*#1^2 + 144*#1^4 & , 4, 0]}, {1/(2*Sqrt[3]), -1/2,
Sqrt[(903 + 350*Sqrt[2] - 223*Sqrt[5] - 282*Sqrt[10])/6]/84 +
Root[1 - 84*#1^2 + 144*#1^4 & , 1, 0]}, {1/(2*Sqrt[3]), 1/2,
Sqrt[(903 + 350*Sqrt[2] - 223*Sqrt[5] - 282*Sqrt[10])/6]/84 +
Root[1 - 84*#1^2 + 144*#1^4 & , 1, 0]}, {1/Sqrt[3], 0,
Sqrt[(903 + 350*Sqrt[2] - 223*Sqrt[5] - 282*Sqrt[10])/6]/84 +
Root[1 - 84*#1^2 + 144*#1^4 & , 4, 0]}, {Root[1 - 9*#1^2 + 9*#1^4 & , 1, 0], 0,
Sqrt[(903 + 350*Sqrt[2] - 223*Sqrt[5] - 282*Sqrt[10])/6]/84 +
Root[1 - 36*#1^2 + 144*#1^4 & , 3, 0]}, {Root[1 - 36*#1^2 + 144*#1^4 & , 4, 0],
(-1 - Sqrt[5])/4, Sqrt[(903 + 350*Sqrt[2] - 223*Sqrt[5] - 282*Sqrt[10])/6]/84 +
Root[1 - 36*#1^2 + 144*#1^4 & , 3, 0]}, {Root[1 - 36*#1^2 + 144*#1^4 & , 4, 0],
(1 + Sqrt[5])/4, Sqrt[(903 + 350*Sqrt[2] - 223*Sqrt[5] - 282*Sqrt[10])/6]/84 +
Root[1 - 36*#1^2 + 144*#1^4 & , 3, 0]}},
Polygon[{{8, 3, 4}, {4, 3, 7}, {4, 7, 10}, {3, 9, 7}, {3, 8, 2, 5, 9}, {6, 2, 8, 4, 10},
{10, 7, 9, 5, 6}, {1, 2, 6}, {1, 6, 5}, {1, 5, 2}}]]]
In[71]:=
![]()
Out[71]=
In[72]:=
![]()
Out[72]=
![]()
In[73]:=
![]()
Out[73]=

Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

