.
Cantellated tesseract
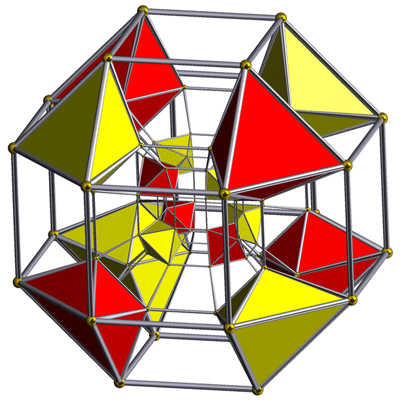
Cantellated tesseract, Schlegel diagram
Centered on rhombicuboctahedron
octahedral cells shown
In geometry, the cantellated tesseract (or bicantellated 16-cell) is a convex uniform polychoron or 4-dimensional polytope bounded by 56 cells: 8 small rhombicuboctahedra, 16 octahedra, and 32 triangular prisms.
Construction
In the process of cantellation, a polytope's 2-faces are effectively shrunk. The rhombicuboctahedron can be called a cantellated cube, since if its six faces are shrunk in their respective planes, each vertex will separate into the three vertices of the rhombicuboctahedron's triangles, and each edge will separate into two of the opposite edges of the rhombicuboctahedrons twelve non-axial squares.
When the same process is applied to the tesseract, each of the eight cubes becomes a rhombicuboctahedron in the described way. In addition however, since each cube's edge was previously shared with two other cubes, the separating edges form the three parallel edges of a triangular prism—32 triangular prisms, since there were 32 edges. Further, since each vertex was previously shared with three other cubes, the vertex would split into 12 rather than three new vertices. However, since some of the shrunken faces continues to be shared, certain pairs of these 12 potential vertices are identical to each other, and therefore only 6 new vertices are created from each original vertex (hence the cantellated tesseract's 96 vertices compared to the tesseract's 16). These six new vertices form the vertices of an octahedron—16 octahedra, since the tesseract had 16 vertices.
Cartesian coordinates
The Cartesian coordinates of the vertices of a cantellated tesseract with edge length 2 is given by all permutations of:
![]()
Structure
The 8 small rhombicuboctahedral cells are joined to each other via their axial square faces. Their non-axial square faces, which correspond with the edges of a cube, are connected to the triangular prisms. The triangular faces of the small rhombicuboctahedra and the triangular prisms are connected to the 16 octahedra.
Its structure can be imagined by means of the tesseract itself: the rhombicuboctahedra are analogous to the tesseract's cells, the triangular prisms are analogous to the tesseract's edges, and the octahedra are analogous to the tesseract's vertices.
Images
Projections
The following is the layout of the cantellated tesseract's cells under the parallel projection into 3-dimensional space, small rhombicuboctahedron first:
* The projection envelope is a truncated cube.
* The nearest and farthest small rhombicuboctahedral cells from the 4D viewpoint project to the volume of the same shape inscribed in the projection envelope.
* The axial squares of this central small rhombicuboctahedron touches the centers of the 6 octagons of the envelope. The octagons are the image of the other 6 small rhombicuboctahedral cells.
* The 12 wedge-shaped volumes connecting the non-axial square faces of the central small rhombicuboctahedron to the neighbouring octagons are the images of 24 of the triangular prisms.
* The remaining 8 triangular prisms project onto the triangular faces of the envelope.
* Between the triangular faces of the envelope and the triangular faces of the central small rhombicuboctahedron are 8 octahedral volumes, which are the images of the 16 octahedral cells.
This layout of cells in projection is analogous to the layout of faces in the projection of the truncated cube into 2 dimensions. Hence, the cantellated tesseract may be thought of as an analogue of the truncated cube in 4 dimensions. (It is not the only possible analogue; another close candidate is the truncated tesseract.)
Another uniform polychoron with a similar layout of cells is the runcitruncated 16-cell.
See also
* tesseract
* runcitruncated 16-cell
* uniform polychoron
External links
* 2. Convex uniform polychora based on the tesseract (8-cell) and hexadecachoron (16-cell) - Model 14, George Olshevsky.
Related uniform polytopes
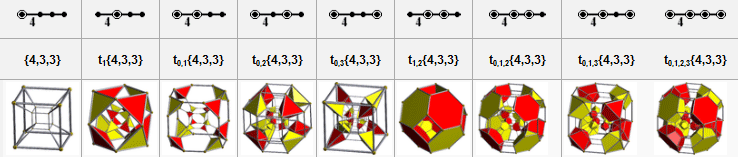
| Name | tesseract | rectified tesseract |
truncated tesseract |
cantellated tesseract |
runcinated tesseract |
bitruncated tesseract |
cantitruncated tesseract |
runcitruncated tesseract |
omnitruncated tesseract |
|---|---|---|---|---|---|---|---|---|---|
| Coxeter-Dynkin diagram |
 |
||||||||
| Schläfli symbol |
|||||||||
| Schlegel diagram |
|||||||||
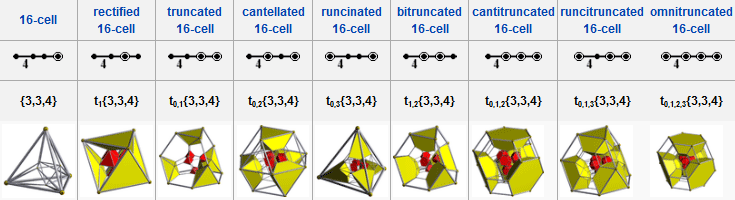
| Name | 16-cell | rectified 16-cell |
truncated 16-cell |
cantellated 16-cell |
runcinated 16-cell |
bitruncated 16-cell |
cantitruncated 16-cell |
runcitruncated 16-cell |
omnitruncated 16-cell |
| Coxeter-Dynkin diagram |
 |
||||||||
| Schläfli symbol |
|||||||||
| Schlegel diagram |
|||||||||
Images: Robert Webb's Great Stella software
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

