In projective geometry, Desargues' theorem, named in honor of Gérard Desargues, states:

In a projective space, two triangles are in perspective axially if and only if they are in perspective centrally.

Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C. Axial perspectivity is the condition satisfied if and only if the point of intersection of ab with AB, and that of intersection of ac with AC, and that of intersection of bc with BC, are collinear, on a line called the axis of perspectivity. Central perspectivity is the condition satisfied if and only if the three lines Aa, Bb, and Cc are concurrent, at a point called the center of perspectivity.

Desargues's theorem holds for any projective space over a field or division ring, and for any projective space of dimension not 2, and for any projective space that can be embedded in a space of dimension at least 3, and for any projective space in which Pappus's theorem holds, but there are some non-Desarguesian planes in which it fails.

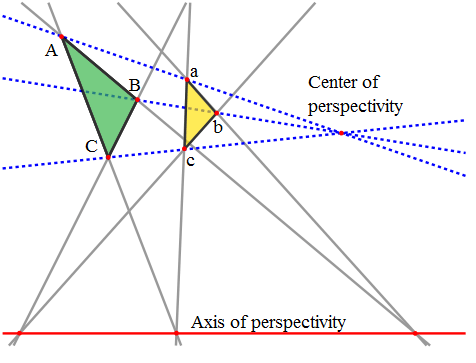
Perspective triangles (*). When produced, corresponding sides of the triangles meet at collinear points along the axis of perspectivity. The lines which run through corresponding vertices on the triangles meet at a point called the center of perspectivity. Desargues' theorem guarantees that the truth of the first condition is necessary and sufficient for the truth of the second.

Projective versus affine spaces

In an affine space a similar statement is true only if one lists various exceptions involving accidentally parallel lines. Desargues' theorem is therefore one of the most basic of simple and intuitive geometric theorems whose natural home is in projective rather than affine space.

Self-duality

By definition, two triangles are perspective if and only if they are in perspective axially (or, equivalently according to this theorem, in perspective centrally). Note that perspective triangles need not be similar.

Under the standard duality of plane projective geometry (where points correspond to lines and collinearity of points corresponds to concurrency of lines), the statement of Desargues's theorem is self-dual: axial perspectivity is translated into central perspectivity and vice versa.

The Desargues configuration
The Desargues configuration viewed as a pair of mutually inscribed pentagons: each pentagon vertex lies on the line through one of the sides of the other pentagon.

The ten lines involved (six sides of triangles, the three lines Aa, Bb, and Cc, and the axis of perspectivity) and the ten points involved (the six vertices, the three points of intersection on the axis of perspectivity, and the center of perspectivity) are so arranged that each of the ten lines passes through three of the ten points, and each of the ten points lies on three of the ten lines. Those ten points and ten lines make up the Desargues configuration (see projective configuration). The statement of the theorem above may misleadingly connote that the Desargues configuration has less symmetry than it really has: Any of the ten points may be chosen to be the center of perspectivity, and that choice determines which six points will be the vertices of triangles and which line will be the axis of perspectivity. The Desargues configuration has symmetry group of order 120 given by the symmetric group on 5 points. It can be constructed from a 5 point set, preserving the action of the symmetric group, by letting the points and lines of the Desargues configuration correspond to 2 and 3 element subsets of the 5 points, with incidence corresponding to containment.

As a projective configuration the Desargues configuration has the notation (103103). Its ten points can be viewed in a unique way as a pair of mutually inscribed pentagons, or as a self-inscribed decagon (Hilbert and Cohn-Vossen 1952). The Desargues graph, a 20-vertex bipartite symmetric cubic graph, is so called because it can be interpreted as the Levi graph of the Desargues configuration, with a vertex for each point and line of the configuration and an edge for every incident point-line pair.

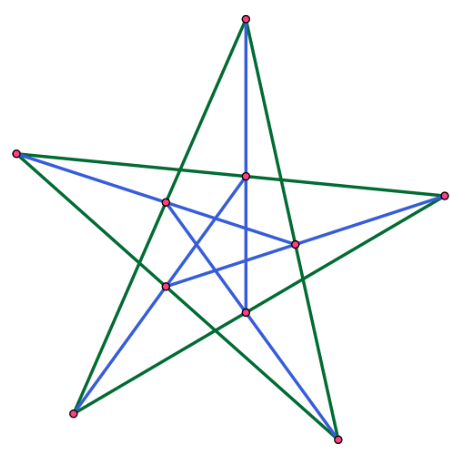
A non-Desargues (103103) configuration.

There also exist eight other (103103) configurations (that is, sets of points and lines in the Euclidean plane with three lines per point and three points per line) that are not incidence-isomorphic to the Desargues configuration, one of which is shown at left. In all of these configurations, any chosen point has three other points that are not collinear with it. But in the Desargues configuration, these three points are always collinear (if the chosen point is the center of perspectivity, then the three points form the axis of perspectivity) while in the other configuration shown in the illustration these three points form a triangle of three lines. As with the Desargues configuration, the other depicted configuration can be viewed as a pair of mutually inscribed pentagons.

Proof of Desargues' theorem

Desargues's theorem holds for projective space of any dimension over any field or division ring, and also holds for abstract projective spaces of dimension at least 3. In dimension 2 the planes for which it holds are called Desarguesian planes and are the same as the planes that can be given coordinates over a division ring. There are also many non-Desarguesian planes where Desargues's theorem does not hold.

Three-dimensional proof

Desargues's theorem is true for any projective space of dimension at least 3, and more generally for any projective space that can be embedded in a space of dimension at least 3.

Desargues' theorem can be stated as follows:

If A.a, B.b, C.c are concurrent, then
(A.B) ∩ (a.b), (A.C) ∩ (a.c), (B.C) ∩ (b.c) are collinear.

The lines (A.B) and (a.b) intersect because they lie in the plane spanned by A, B, a, b, and the point of intersection lies in the intersection of the planes containing the green and yellow triangles because (A.B) lies in the plane of one triangle and (a.b) lies in the plane of the other. So (A.B) ∩ (a.b) is contained in the intersection of these two planes, and by symmetry so are the other two points (A.C) ∩ (a.c), (B.C) ∩ (b.c).

This proves Desargues's theorem if the two triangles are not contained in the same plane, as the intersection of their planes is then a line, and contains the three points. If they are in the same plane, Desargues's theorem can be proved by choosing a point not in the plane, using this to lift the triangles out of the plane so that the argument above works, and then projecting back into the plane. The last step of the proof fails if the projective space has dimension less than 3, as in this case it may not be possible to find a point outside the plane.

Monge's theorem also asserts that three points lie on a line, and has a proof using the same idea of considering it in three rather than two dimensions and writing the line as an intersection of two planes.

Two-dimensional proof

As there are non-Desarguesian projective planes in which Desargues theorem is not true, some extra condition needs to be assumed in order to prove it. Hessenberg (1905) showed that Desargues's theorem can be deduced from Pappus's theorem by three applications of it (Coxeter 1969, 14.3).

References

* Coxeter, Harold Scott MacDonald (1969), Introduction to Geometry (2nd ed.), New York: John Wiley & Sons, MR123930, ISBN 978-0-471-50458-0
* Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), Chelsea, pp. 119–128, ISBN 0-8284-1087-9
* Hessenberg, Gerhard (1905), "Beweis des Desarguesschen Satzes aus dem Pascalschen", Mathematische Annalen (Berlin / Heidelberg: Springer) 61 (2): 161–172, doi:10.1007/BF01457558, ISSN 1432-1807
* Voitsekhovskii, M.I. (2001), "Desargues assumption", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de/d/d031320.htm

External links

* Desargues Theorem at MathWorld
* Desargues' Theorem at cut-the-knot
* Monge via Desargues at cut-the-knot
* Alternate proof of Desargues' theorem at PlanetMath
* Desargues' Theorem at Dynamic Geometry Sketches