.
Fermat point
In geometry the Fermat point of a triangle, also called Torricelli point, is a point such that the total distance from the three vertices of the triangle to the point is the minimum possible.[1] It is so named because this problem is first raised by Fermat in a private letter to Evangelista Torricelli, who solved it.
The Fermat point gives a solution to the geometric median and Steiner tree problems for three points.
Construction
In order to locate the Fermat point of a triangle with largest angle at most 120°:
Construct two equilateral triangles on any of the three sides of the given triangle.
For each new vertex of the equilateral triangle, draw a line from it to the opposite triangle's vertex.
The two lines intersect at the Fermat point.
An alternate method is the following:
On any two of the three sides, construct two isosceles triangles, with base the side in question, 30-degree angles at the base, and vertices laying outside the original triangle.
Draw two circles, each with center on the vertex of the just constructed isosceles triangles and radius the identical side of the isosceles triangles.
The intersection inside the original triangle between the two circles is the Fermat point.
When a triangle has an angle greater than 120° the Fermat point is sited at the obtuse angled vertex.
The Fermat point has a near-identical twin called the first isogonic center or X(13) and it is important not to confuse the two. Their relationship is explored below.
Geometry
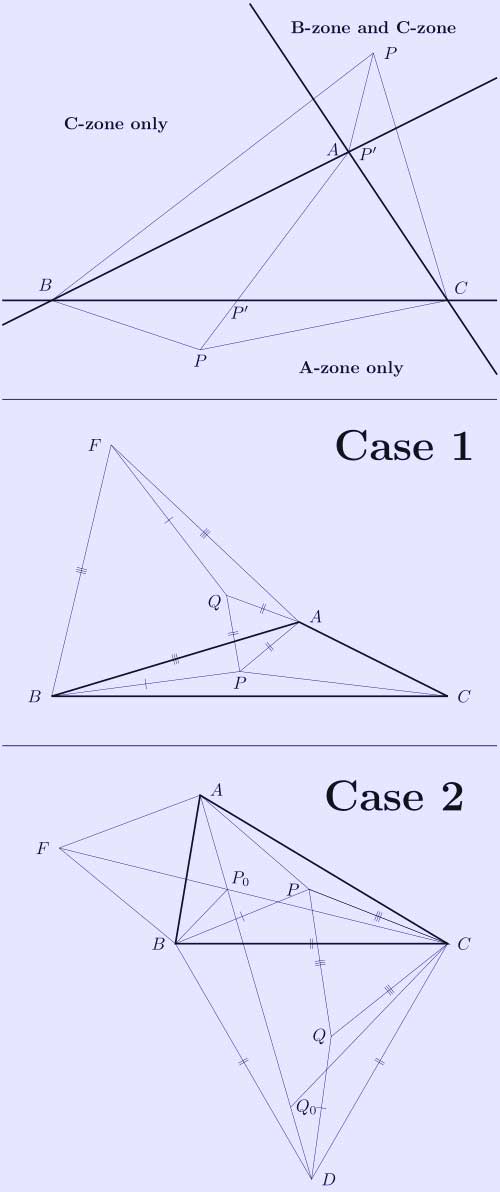
Fig 2. Geometry of the Fermat point
Given any Euclidean triangle ABC and an arbitrary point P let d(P) = PA+PB+PC. The aim of this section is to identify a point P0 such that d(P0) < d(P) for all P ≠ P0. If such a point exists then it will be the Fermat point. In what follows Δ will denote the points inside the triangle and will be taken to include its boundary Ω.
A key result that will be used is the dogleg rule which asserts that if a triangle and a polygon have one side in common and the rest of the triangle lies inside the polygon then the triangle has a shorter perimeter than the polygon.
[ If AB is the common side extend AC to cut the polygon at X. Then by the triangle inequality the polygon perimeter > AB+AX+XB = AB+AC+CX+XB ≥ AB+AC+BC. ]
Let P be any point outside Δ. Associate each vertex with its remote zone; that is, the half-plane beyond the (extended) opposite side. These 3 zones cover the entire plane except for Δ itself and P clearly lies in either one or two of them. If P is in two (say the B and C zones intersection) then setting P' = A implies d(P') = d(A) < d(P) by the dogleg rule. Alternatively if P is in only one zone, say the A-zone, then d(P') < d(P) where P' is the intersection of AP and BC. So for every point P outside Δ there exists a point P' in Ω such that d(P') < d(P).
Case 1. The triangle has an angle ≥ 120°.
Without loss of generality suppose that the angle at A is ≥ 120°. Construct the equilateral triangle AFB and for any point P in Δ (except A itself) construct Q so that the triangle AQP is equilateral and has the orientation shown. Then the triangle ABP is a 60° rotation of the triangle AFQ about A so these two triangles are congruent and it follows that d(P) = CP+PQ+QF which is simply the length of the path CPQF. As P is constrained to lie within ABC, by the dogleg rule the length of this path exceeds AC+AF = d(A). Therefore d(A) < d(P) for all P є Δ, P ≠ A. Now allow P to range outside Δ. From above a point P' є Ω exists such that d(P') < d(P) and as d(A) ≤ d (P') it follows that d(A) < d(P) for all P outside Δ. Thus d(A) < d(P) for all P ≠ A which means that A is the Fermat point of Δ. In other words the Fermat point lies at the obtuse angled vertex.
Case 2. The triangle has no angle ≥ 120°.
Let P be any point inside Δ and construct the equilateral triangle CPQ. Then CQD is a 60° rotation of CPB about C so d(P) = PA+PB+PC = AP+PQ+QD which is simply the length of the path APQD. Let P0 be the point where AD and CF intersect. This point is commonly called the first isogonic center. By the angular restriction P0 lies inside Δ moreover BCF is a 60° rotation of BDA about B so Q0 must lie somewhere on AD. Since CDB = 60° it follows that Q0 lies between P0 and D which means AP0Q0D is a straight line so d(P0) = AD. Moreover if P ≠ P0 then either P or Q won't lie on AD which means d(P0) = AD < d(P). Now allow P to range outside Δ. From above a point P' є Ω exists such that d(P') < d(P) and as d(P0) ≤ d(P') it follows that d(P0) < d(P) for all P outside Δ. That means P0 is the Fermat point of Δ. In other words the Fermat point is coincident with the first isogonic center.
Concurrency
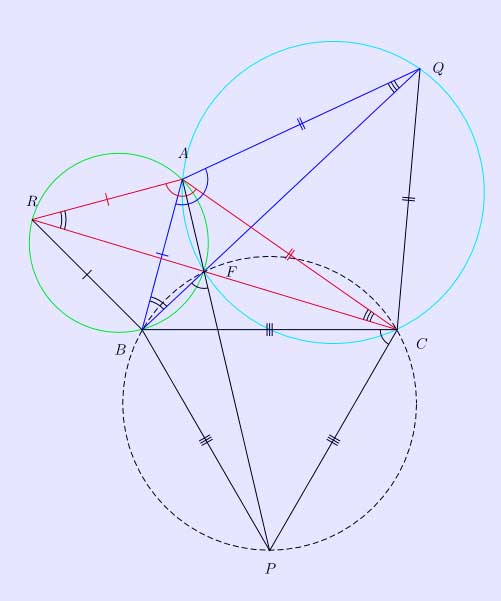
Fig 3. Geometry of the first isogonic center.
Here is a proof using properties of concyclic points to show that the three red lines in Fig 1 are concurrent and cut one another at angles of 60°.
In Fig 3 suppose RC and BQ intersect at F, and two lines, AF and FP, are drawn. We aim to prove that the points A,F,P are collinear.
The triangles RAC and BAQ are congruent because the second is a 60° rotation of the first about A. Hence ∠ARF = ∠ABF and ∠AQF = ∠ACF. By converse of angle in the same segment, ARBF and AFCQ are both concyclic. Thus ∠AFB = ∠AFC = ∠BFC = 120°. Because ∠BFC and ∠BPC add up to 180°, BPCF is also concyclic. Hence ∠BFP = ∠BCP = 60°. Because ∠BFP + ∠BFA = 180°, AFP is a straight line.
Q.E.D.
This proof only applies in Case 2 since if ∠BAC > 120° A lies inside the circumcircle of BPC which switches the relative positions of A and F. However it is easily modified to cover Case 1. Then ∠AFB = ∠AFC = 60° hence ∠BFC = ∠AFB = ∠AFC = 120° which means BPCF is concyclic so ∠BFP = ∠BCP = 60° = ∠BFA. Therefore A lies on FP.
Clearly any 3 lines perpendicular to the red ones in Fig 1, in particular those joining the centres of the circles, must also cut at angles of 60° and thereby form an equilateral triangle. This curiosity is known as Napoleon's Theorem.
Another proof
Another approach to find a point within the triangle, from where sum of the distances to the vertices of triangle is minimum, is to use one of the optimization (mathematics) methods. In particular, method of the lagrange multipliers and the law of cosines.
We draw lines from the point within the triangle to its vertices and call them X, Y and Z. Also, let the lengths of these lines be x, y, and z, respectively. Let the acute angle between X and Y be α, Y and Z be β. Then the angle between X and Z is (2π − α − β). Using the method of lagrange multipiers we have to find the minimum of the lagrangian, which is expressed as:
- x + y + z +
- λ1 (x2 + y2 − 2xy cos(α) − a2) +
- λ2 (y2 + z2 − 2yz cos(β) − b2) +
- λ3 (z2 + x2 − 2zx cos(α + β) − c2) .
where a, b and c are the lengths of the sides of the triangle.
Calculating the partial derivatives δ/δx, δ/δy, δ/δz, δ/δα, δ/δβ gives a system of 5 equations:
- δ/δx: 1 + λ1(2x − 2y cos(α)) + λ3(2x − 2z cos(α + β)) = 0
- δ/δy: 1 + λ1(2y − 2x cos(α)) + λ2(2y − 2z cos(β)) = 0
- δ/δz: 1 + λ2(2z − 2y cos(β)) + λ3(2z − 2x cos(α + β)) = 0
- δ/δα: λ1y sin(α) + λ3z sin(α + β) = 0
- δ/δβ: λ2y sin(β) + λ3x sin(α + β) = 0
After some algebraic manipulations equations for α and β separate from the rest of the parameters, giving:
sin(α) = sin(β)
sin(α + β) = −sin(β)
that gives: α = β = 120°
Q.E.D.
Note: if one of the vertices of triangle has angle not less than 120°, then the Fermat point is at that vertex.
Properties
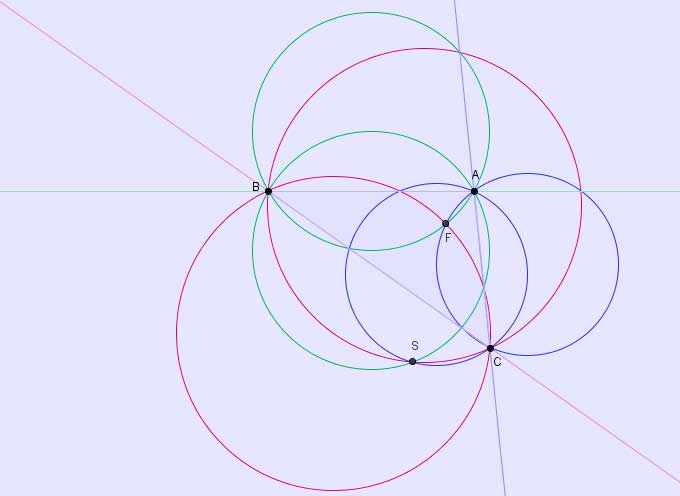
The two isogonic centers are the intersections of three vesicae piscis whose paired vertices are the vertices of the triangle
When the largest angle of the triangle is not larger than 120°, X(13) is the Fermat point.
The angles subtended by the sides of the triangle at X(13) are all equal to 120° (Case 2), or 60°, 60°, 120° (Case 1).
The circumcircles of the three regular triangles in the construction intersect at X(13).
Trilinear coordinates for the first isogonic center, X(13):
csc(A + π/3) : csc(B + π/3) : csc(C + π/3), or, equivalently,
sec(A − π/6) : sec(B − π/6) : sec(C − π/6).[2]
Trilinear coordinates for the second isogonic center, X(14):
csc(A − π/3) : csc(B − π/3) : csc(C − π/3), or, equivalently,
sec(A + π/6) : sec(B + π/6) : sec(C + π/6).[3]
Trilinear coordinates for the Fermat point:
1 − u + uvw sec(A − π/6) : 1 − v + uvw sec(B − π/6) : 1 − w + uvw sec(C − π/6)
where u, v, w respectively denote the Boolean variables (A<120°), (B<120°), (C<120°).
The isogonal conjugate of X(13) is the first isodynamic point, X(15):
sin(A + π/3) : sin(B + π/3) : sin(C + π/3).[4]
The isogonal conjugate of X(14) is the second isodynamic point, X(16):
sin(A − π/3) : sin(B − π/3) : sin(C − π/3).[5]
The following triangles are equilateral:
antipedal triangle of X(13)
antipedal triangle of X(14)
pedal triangle of X(15)
pedal triangle of X(16)
circumcevian triangle of X(15)
circumcevian triangle of X(16)
The lines X(13)X(15) and X(14)X(16) are parallel to the Euler line. The three lines meet at the Euler infinity point, X(30).
The points X(13), X(14), circumcenter, nine-point center lie on a Lester circle.
Aliases
X(13) and X(14) are also known as the first Fermat point and the second Fermat point respectively. Alternatives are the positive Fermat point and the negative Fermat point. However all these different names can be confusing and are perhaps best avoided. The problem is that much of the literature blurs the distinction between the Fermat point and the first Fermat point whereas it is only in Case 2 above that they are actually the same.
History
This question was proposed by Fermat, as a challenge to Evangelista Torricelli. He solved the problem in a similar way to Fermat's, albeit using intersection of the circumcircles of the three regular triangles instead. His pupil, Viviani, published the solution in 1659.[6]
See also
Geometric median or Fermat–Weber point, the point minimizing the sum of distances to more than three given points.
Lester's theorem
Triangle center
References
^ Cut The Knot - The Fermat Point and Generalizations
^ Entry X(13) in the Encyclopedia of Triangle Centers
^ Entry X(14) in the Encyclopedia of Triangle Centers
^ Entry X(15) in the Encyclopedia of Triangle Centers
^ Entry X(16) in the Encyclopedia of Triangle Centers
^ Weisstein, Eric W., "Fermat Points" from MathWorld.
External links
Fermat Point by Chris Boucher, The Wolfram Demonstrations Project.
Fermat-Torricelli generalization at Dynamic Geometry Sketches Interactive sketch generalizes the Fermat-Torricelli point.
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

