.
Golden rectangle
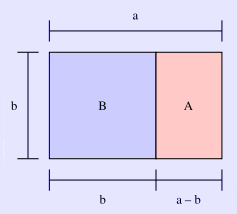
The large rectangle BA is a golden rectangle; that is, the proportion b:a is 1: ![]() . For any such rectangle, and only for rectangles of that specific proportion, if we remove square B, what is left, A, is another golden rectangle; that is, with the same proportions as the original rectangle.
. For any such rectangle, and only for rectangles of that specific proportion, if we remove square B, what is left, A, is another golden rectangle; that is, with the same proportions as the original rectangle.
A golden rectangle is a rectangle whose side lengths are in the golden ratio, 1 : ![]() (one-to-phi), that is, approximately 1:1.618.
(one-to-phi), that is, approximately 1:1.618.
A distinctive feature of this shape is that when a square section is removed, the remainder is another golden rectangle, that is, with the same proportions as the first. Square removal can be repeated infinitely, which leads to an approximation of the golden spiral.

According to astrophysicist and math popularizer Mario Livio, since the publication of Luca Pacioli's Divina Proportione in 1509,[1] when "with Pacioli's book, the Golden Ratio started to become available to artists in theoretical treatises that were not overly mathematical, that they could actually use,"[2] many artists and architects have proportioned their works to approximate the form of the golden rectangle, which has been considered aesthetically pleasing. The proportions of the golden rectangle have been observed in works predating Pacioli's publication.[3]

Constructing a golden rectangle
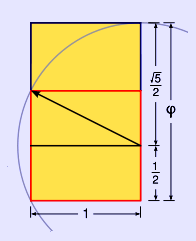
A method to construct a golden rectangle. The resulting dimensions are in the ratio 1 : ![]() , the golden ratio
, the golden ratio
A golden rectangle can be constructed with only straightedge and compass by this technique:
1. Construct a simple square
2. Draw a line from the midpoint of one side of the square to an opposite corner
3. Use that line as the radius to draw an arc that defines the height of the rectangle
4. Complete the golden rectangle
Applications of the golden rectangle
* Jan Tschichold describes the use of the golden rectangle in medieval book designs
* Le Corbusier's 1927 Villa Stein in Garches features a rectangular ground plan, elevation, and inner structure that are closely approximate to golden rectangles.[4]
See also
* Leonardo of Pisa
* Fibonacci numbers
* Kepler triangle
References
1. ^ Pacioli, Luca. De divina proportione, Luca Paganinem de Paganinus de Brescia (Antonio Capella) 1509, Venice.
2. ^ Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York: Broadway Books. ISBN 0-7679-0815-5.
3. ^ Van Mersbergen, Audrey M., Rhetorical Prototypes in Architecture: Measuring the Acropolis with a Philosophical Polemic, Communication Quarterly, Vol. 46, 1998 ("a 'Golden Rectangle' has a ratio of the length of its sides equal to 1:1.61803+. The Parthenon is of these dimensions.")
4. ^ Le Corbusier, The Modulor, p. 35, as cited in Padovan, Richard, Proportion: Philosophy, Science and Architecture (1999), p. 320. Taylor & Francis. ISBN 0-419-22780-6: "Both the paintings and the architectural designs make use of the golden section".
Links
# The Golden Mean and the Physics of Aesthetics
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

