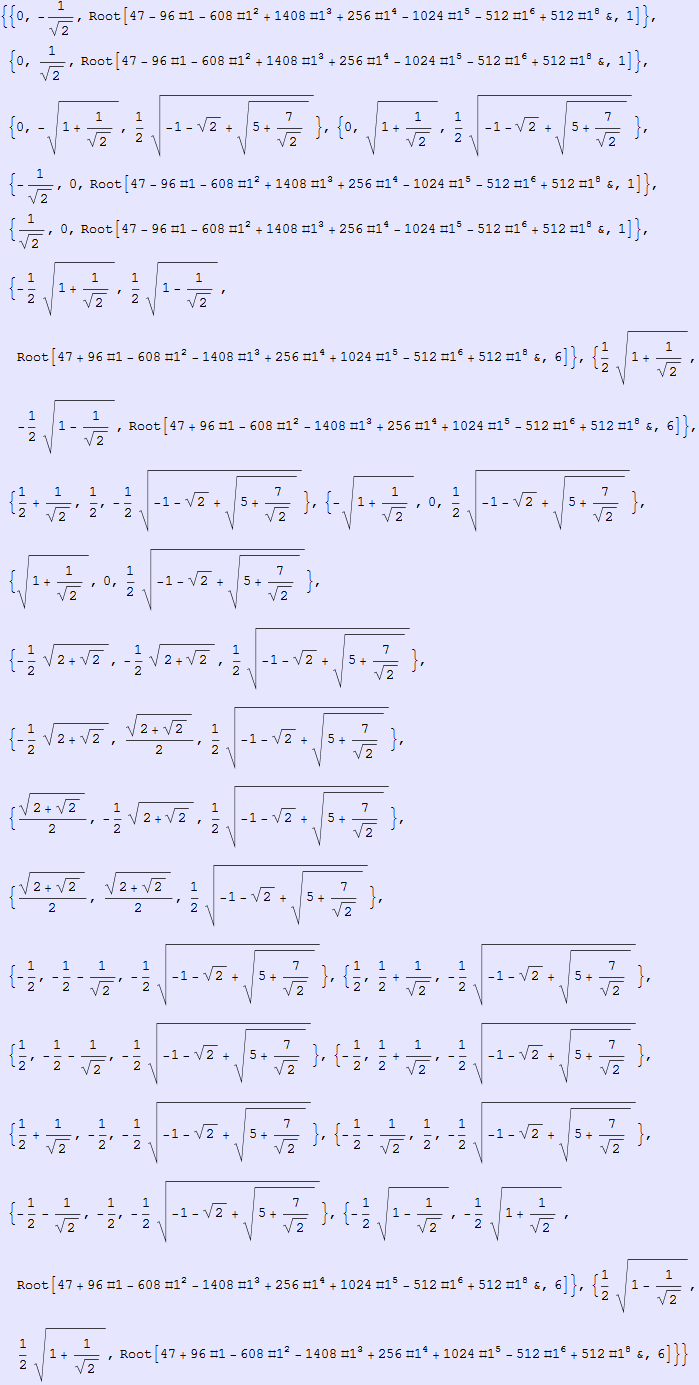In[602]:=
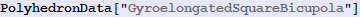
Out[602]=
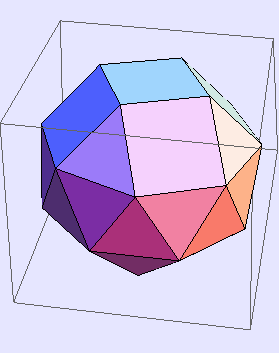
In[603]:=
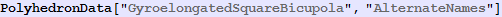
Out[603]=
In[604]:=

Out[604]=
In[605]:=
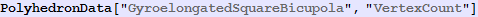
Out[605]=
In[606]:=

Out[606]=
In[607]:=
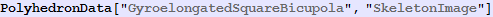
Out[607]=
In[608]:=
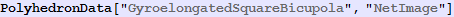
Out[608]=
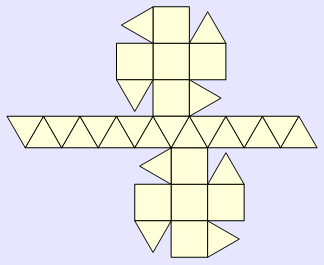
In[609]:=
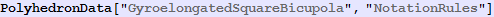
Out[609]=
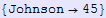
In[610]:=
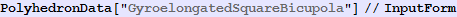
Out[610]//InputForm=
Graphics3D[GraphicsComplex[
{{0, -(1/Sqrt[2]), Root[47 - 96*#1 - 608*#1^2 + 1408*#1^3 + 256*#1^4 - 1024*#1^5 - 512*#1^6 + 512*#1^8 & ,
1, 0]}, {0, 1/Sqrt[2], Root[47 - 96*#1 - 608*#1^2 + 1408*#1^3 + 256*#1^4 - 1024*#1^5 - 512*#1^6 +
512*#1^8 & , 1, 0]}, {0, -Sqrt[1 + 1/Sqrt[2]], Sqrt[-1 - Sqrt[2] + Sqrt[5 + 7/Sqrt[2]]]/2},
{0, Sqrt[1 + 1/Sqrt[2]], Sqrt[-1 - Sqrt[2] + Sqrt[5 + 7/Sqrt[2]]]/2},
{-(1/Sqrt[2]), 0, Root[47 - 96*#1 - 608*#1^2 + 1408*#1^3 + 256*#1^4 - 1024*#1^5 - 512*#1^6 + 512*#1^8 & ,
1, 0]}, {1/Sqrt[2], 0, Root[47 - 96*#1 - 608*#1^2 + 1408*#1^3 + 256*#1^4 - 1024*#1^5 - 512*#1^6 +
512*#1^8 & , 1, 0]}, {-Sqrt[1 + 1/Sqrt[2]]/2, Sqrt[1 - 1/Sqrt[2]]/2,
Root[47 + 96*#1 - 608*#1^2 - 1408*#1^3 + 256*#1^4 + 1024*#1^5 - 512*#1^6 + 512*#1^8 & , 6, 0]},
{Sqrt[1 + 1/Sqrt[2]]/2, -Sqrt[1 - 1/Sqrt[2]]/2,
Root[47 + 96*#1 - 608*#1^2 - 1408*#1^3 + 256*#1^4 + 1024*#1^5 - 512*#1^6 + 512*#1^8 & , 6, 0]},
{1/2 + 1/Sqrt[2], 1/2, -Sqrt[-1 - Sqrt[2] + Sqrt[5 + 7/Sqrt[2]]]/2},
{-Sqrt[1 + 1/Sqrt[2]], 0, Sqrt[-1 - Sqrt[2] + Sqrt[5 + 7/Sqrt[2]]]/2},
{Sqrt[1 + 1/Sqrt[2]], 0, Sqrt[-1 - Sqrt[2] + Sqrt[5 + 7/Sqrt[2]]]/2},
{-Sqrt[2 + Sqrt[2]]/2, -Sqrt[2 + Sqrt[2]]/2, Sqrt[-1 - Sqrt[2] + Sqrt[5 + 7/Sqrt[2]]]/2},
{-Sqrt[2 + Sqrt[2]]/2, Sqrt[2 + Sqrt[2]]/2, Sqrt[-1 - Sqrt[2] + Sqrt[5 + 7/Sqrt[2]]]/2},
{Sqrt[2 + Sqrt[2]]/2, -Sqrt[2 + Sqrt[2]]/2, Sqrt[-1 - Sqrt[2] + Sqrt[5 + 7/Sqrt[2]]]/2},
{Sqrt[2 + Sqrt[2]]/2, Sqrt[2 + Sqrt[2]]/2, Sqrt[-1 - Sqrt[2] + Sqrt[5 + 7/Sqrt[2]]]/2},
{-1/2, -1/2 - 1/Sqrt[2], -Sqrt[-1 - Sqrt[2] + Sqrt[5 + 7/Sqrt[2]]]/2},
{1/2, 1/2 + 1/Sqrt[2], -Sqrt[-1 - Sqrt[2] + Sqrt[5 + 7/Sqrt[2]]]/2},
{1/2, -1/2 - 1/Sqrt[2], -Sqrt[-1 - Sqrt[2] + Sqrt[5 + 7/Sqrt[2]]]/2},
{-1/2, 1/2 + 1/Sqrt[2], -Sqrt[-1 - Sqrt[2] + Sqrt[5 + 7/Sqrt[2]]]/2},
{1/2 + 1/Sqrt[2], -1/2, -Sqrt[-1 - Sqrt[2] + Sqrt[5 + 7/Sqrt[2]]]/2},
{-1/2 - 1/Sqrt[2], 1/2, -Sqrt[-1 - Sqrt[2] + Sqrt[5 + 7/Sqrt[2]]]/2},
{-1/2 - 1/Sqrt[2], -1/2, -Sqrt[-1 - Sqrt[2] + Sqrt[5 + 7/Sqrt[2]]]/2},
{-Sqrt[1 - 1/Sqrt[2]]/2, -Sqrt[1 + 1/Sqrt[2]]/2,
Root[47 + 96*#1 - 608*#1^2 - 1408*#1^3 + 256*#1^4 + 1024*#1^5 - 512*#1^6 + 512*#1^8 & , 6, 0]},
{Sqrt[1 - 1/Sqrt[2]]/2, Sqrt[1 + 1/Sqrt[2]]/2,
Root[47 + 96*#1 - 608*#1^2 - 1408*#1^3 + 256*#1^4 + 1024*#1^5 - 512*#1^6 + 512*#1^8 & , 6, 0]}},
Polygon[{{9, 15, 11}, {17, 4, 15}, {19, 13, 4}, {21, 10, 13}, {22, 12, 10}, {16, 3, 12}, {18, 14, 3},
{20, 11, 14}, {9, 17, 15}, {17, 19, 4}, {19, 21, 13}, {21, 22, 10}, {22, 16, 12}, {16, 18, 3},
{18, 20, 14}, {20, 9, 11}, {24, 7, 23, 8}, {7, 24, 4, 13}, {23, 7, 10, 12}, {8, 23, 3, 14},
{24, 8, 11, 15}, {15, 4, 24}, {13, 10, 7}, {12, 3, 23}, {14, 11, 8}, {5, 2, 6, 1}, {20, 18, 1, 6},
{17, 9, 6, 2}, {21, 19, 2, 5}, {16, 22, 5, 1}, {1, 18, 16}, {6, 9, 20}, {2, 19, 17}, {5, 22, 21}}]]]
In[611]:=
Out[611]=
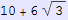
In[612]:=

Out[612]=
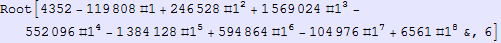
In[613]:=

Out[613]=
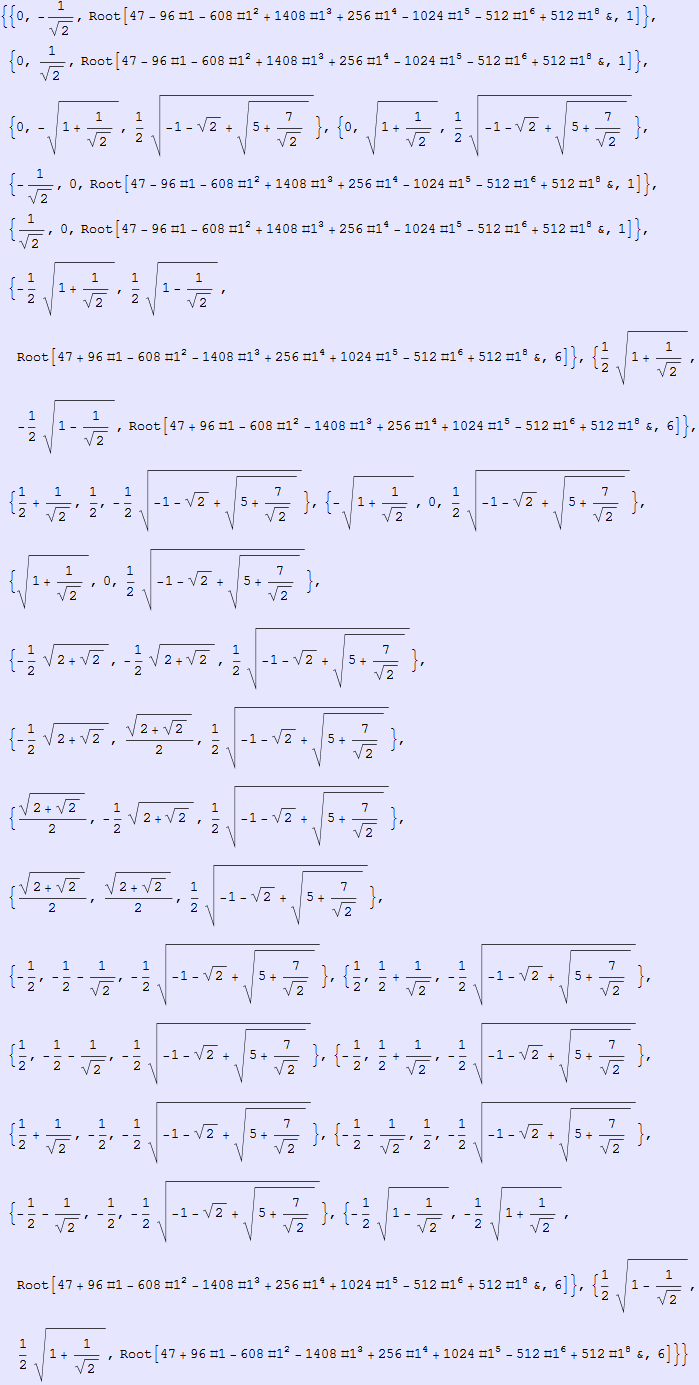
Johnson Polyhedra
Geometry