Heptagon

Regular Heptagon

Regular heptagon
Edges and vertices	7
Schläfli symbol	{7}
Coxeter–Dynkin diagram
Symmetry group	Dihedral (D₇)
Area (with t=edge length)
Internal angle (degrees)	128.5714286°

In geometry, a heptagon is a polygon with seven sides and seven angles. In a regular heptagon, in which all sides and all angles are equal, the sides meet at an angle of 5π/7 radians, 128.5714286 degrees. Its Schläfli symbol is {7}. The area of a regular heptagon of side length a is given by

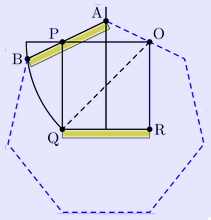
The heptagon is also sometimes referred to as the septagon, using "sept-" (an elision of septua-, a Latin-derived numerical prefix, rather than hepta-, a Greek-derived numerical prefix). The OED lists "septagon" as meaning "heptagonal".

Construction

A regular heptagon is not constructible with compass and straightedge but is constructible with a marked ruler and compass. This type of construction is called a Neusis construction. It is also constructible with compass, straightedge and angle trisector. The impossibility of straightedge and compass construction follows from the observation that 2cos(2π/7) ≈ 1.247 is a zero of the irreducible cubic x³ + x² - 2x - 1. Consequently this polynomial is the minimal polynomial of 2cos(2π/7), whereas the degree of the minimal polynomial for a constructible number must be a power of 2.

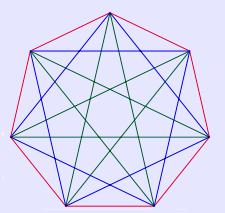
A Neusis construction of the interior angle in a regular heptagon.
A Neusis construction of the interior angle in a regular heptagon.

Heptagrams

Two kinds of heptagrams can be constructed from regular heptagons, labeled by Schläfli symbols {7/2}, and {7/3}, with the divisor being the interval of connection.

Blue, {7/2} and green {7/3} heptagrams inside a red heptagon.

Uses

The United Kingdom currently (2006) has two heptagonal coins, the 50p and 20p pieces, and the Barbados Dollar is also heptagonal. The 20 eurocent coin has cavities placed similarly. Strictly, the shape of the coins is a curvilinear heptagon to make them curves of constant width: the sides are curved outwards so that the coin will roll smoothly in vending machines. The Brazilian 25 cents coin has a heptagon inscribed in the coin's disk.