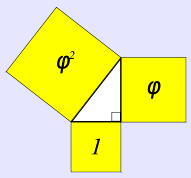
A Kepler triangle is a right triangle with edge lengths in geometric progression. The ratio of the edges of a Kepler triangle are linked to the golden ratio

and can be written: , or approximately 1 : 1.2720196 : 1.6180339.[1]

Triangles with such ratios are named after the German mathematician and astronomer Johannes Kepler (1571–1630) who first demonstrated that a right triangle with edges in geometric progression are characterised by a geometric factor linked to the golden ratio. Kepler triangles combine two key mathematical concepts -- the Pythagorean theorem and the Golden ratio -- that fascinated Kepler deeply, as expressed in the quote:

"Geometry has two great treasures: one is the theorem of Pythagoras, the other the division of a line into mean and extreme ratios, that is , the Golden Mean. The first way may be compared to a measure of gold, the second to a precious jewel."

A triangle with dimensions closely approximating a Kepler triangle can be recognised in the Great Pyramid of Giza.[2] [3] Whether the relationship to the golden ratio in this pyramid occurs by design or by accident remains a topic of controversy.[4]

Derivation

The fact that a triangle with edges 1, and , forms a right triangle follows directly from rewriting the defining quadratic polynomial for the golden ratio \varphi:

into Pythagorean form:

.

Constructing a Kepler triangle

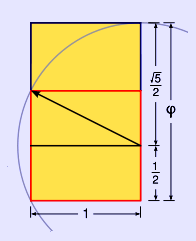
A method to construct a golden rectangle. The resulting dimensions are in the ratio 1 : , the golden ratio

A Kepler triangle can be constructed with only straightedge and compass by first creating a golden rectangle:

1. Construct a simple square

2. Draw a line from the midpoint of one side of the square to an opposite corner

3. Use that line as the radius to draw an arc that defines the height of the rectangle

4. Complete the golden rectangle

5. Use the longer side of the golden triangle to draw an arc that intersects the opposite side of the rectangle and defines the longer rectangular edge of the Kepler triangle

See also

* Golden triangle

References

1. ^ Roger Herz-Fischler (2000). The Shape of the Great Pyramid. Wilfrid Laurier University Press. ISBN 0889203245.

2. ^ (2006) The Best of Astraea: 17 Articles on Science, History and Philosophy. Astrea Web Radio. ISBN 1425970400.

3. ^ Squaring the circle, Paul Calter

4. ^ See the golden ratio article for more detail.

Geometry