.
Monge's theorem
In geometry, Monge's theorem, named after Gaspard Monge, states that for any three circles in a plane, none of which is inside one of the others, the three intersection points of the three pairs of external tangent lines are in fact collinear.
(For any two circles in a plane, an external tangent is a line that is tangent to both circles but does not pass between them. There are two such external tangent lines for any two circles. In other words the two lines which form an "ice-cream cone" which "holds" the two circles.)
Monge's theorem lets us know that surprisingly the three "points" of the "ice-cream cones" are always in a straight line. In the visual example below the red, green, and blue points are all in a straight line.
(In the case of two of the circles being of equal size: the two external tangent lines are of course parallel. In this case Monge's theorem asserts that the other two intersection points must lie on a line parallel to those two external tangents. In other words if the two external tangents are considered to intersect at the point at infinity, then the other two intersection points must be on a line passing through the same point at infinity.)
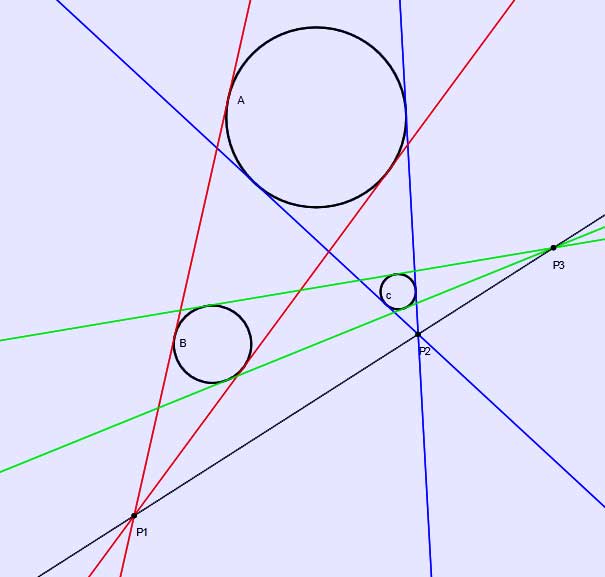
Illustration of Monge's theorem. Circles A, B, and C, determine three collinear points P1, P2, and P3.
Proofs
The simplest proof employs a three-dimensional analogy.[1] Let the three circles correspond to three spheres of the same radii; the circles correspond to the equators that result from a plane passing through the centers of the spheres. The three spheres can be sandwiched uniquely between two planes. Each pair of spheres defines a cone that is externally tangent to both spheres, and the apex of this cone corresponds to the intersection point of the two external tangents, i.e., the external homothetic center. Since one line of the cone lies in each plane, the apex of each cone must lie in both planes, and hence somewhere on the line of intersection of the two planes. Therefore, the three external homothetic centers are collinear.
Monge's theorem can also be proved by using Desargues' theorem. Another easy proof is using Menelaus' theorem, since the ratios can be calculated with the diameters of each circle, which will be eliminated by cyclic forms when using the Menelaus' theorem. Desargues' theorem also asserts that 3 points lie on a line, and has a similar proof using the same idea of considering it in 3 rather than 2 dimensions and writing the line as an intersection of 2 planes.
Bibliography
Graham IA (1959). Ingenious Problems and Methods. New York: Dover Publications.
Wells D (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. pp. pp. 153–154. ISBN 0-14-011813-6.
References
^ Wells, pp. 153–154
External links
Monge's Circle Theorem at MathWorld
Monge's theorem at cut-the-knot
Three Circles and Common Tangents at cut-the-knot
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

