In the mathematical field of group theory, the Monster group M or F1 (also known as the Fischer-Griess Monster, or the Friendly Giant) is a group of finite order

  2⁴⁶ · 3²⁰ · 5⁹ · 7⁶ · 11² · 13³ · 17 · 19 · 23 · 29 · 31 · 41 · 47 · 59 · 71
= 808017424794512875886459904961710757005754368000000000
≈ 8 · 10⁵³.

It is a simple group, meaning it does not have any normal subgroups except for the subgroup consisting only of the identity element, and M itself.

The finite simple groups have been completely classified (the classification of finite simple groups). The list of finite simple groups consists of 18 countably infinite families, plus 26 sporadic groups that do not follow such a systematic pattern. The Monster group is the largest of these sporadic groups and contains all but six of the other sporadic groups as subquotients. Robert Griess has called these six exceptions pariahs, and refers to the others as the happy family.

Existence and uniqueness

The Monster was predicted by Bernd Fischer and Robert Griess in autumn 1973, as a simple group containing, as subquotients, the Fischer groups and some other sporadic simple groups. Within a few months the order of M was estimated by Fischer, Conway, Norton and Thompson, and they discovered other properties and potential subgroups, assuming it existed. Griess first constructed M in 1980 as the automorphism group of the Griess algebra, a 196884-dimensional commutative nonassociative algebra. John Conway and Jacques Tits subsequently simplified this construction.

Griess's construction showed that the Monster existed. John G. Thompson showed that its uniqueness (as a simple group of the given order) would follow from the existence of a 196883-dimensional faithful representation. A proof of the existence of such a representation was announced in 1982 by Simon P. Norton, though he has never published the details. The first published proof of the uniqueness of the Monster was completed by Griess, Meierfrankenfeld, and Segev in 1990.

The character table of the Monster, a 194-by-194 array, was calculated in 1979, before the Monster was proved either to exist or be unique. The calculation was based on the assumption that the minimal degree of a faithful complex representation is 196883, which is the product of the 3 largest prime divisors of the order of M.

Moonshine

The Monster group is one of two principal constituents in the Monstrous moonshine conjecture by Conway and Norton, which relates discrete and non-discrete mathematics and was finally proved by Richard Borcherds in 1992.

In this setting, the Monster group is visible as the automorphism group of the Monster module, a vertex operator algebra, an infinite dimensional algebra containing the Griess algebra, and acts on the Monster Lie algebra, a generalized Kac-Moody algebra.

McKay's E8 observation

There are also connections between the monster and the extended Dynkin diagrams , specifically between the nodes of the diagram and certain conjugacy classes in the monster, known as McKay's E8 observation.[1][2] This is then extended to a relation between the extended diagrams and the groups 3.Fi₂₄', 2.B, and M, where these are (3/2/1-fold central extensions) of the Fischer group, baby monster group, and monster. Note that these are the three largest sporadic groups, and that the order of the extension corresponds to the symmetries of the diagram. See ADE classification: trinities for further connections (of McKay correspondence type), including (for the monster) with the rather small simple group PSL(2,11) and with the 120 tritangent planes of a canonic sextic curve of genus 4.

A computer construction

Robert A. Wilson has found explicitly (with the aid of a computer) two 196882 by 196882 matrices (with elements in the field of order 2) which together generate the Monster group; note that this is dimension 1 lower than the 196883-dimensional representation in characteristic 0. However, performing calculations with these matrices is prohibitively expensive in terms of time and storage space. Wilson with collaborators has found a method of performing calculations with the Monster that is considerably faster.

Let V be a 196882 dimensional vector space over the field with 2 elements. A large subgroup H (preferably a maximal subgroup) of the Monster is selected in which it is easy to perform calculations. The subgroup H chosen is 31+12.2.Suz.2, where Suz is the Suzuki group. Elements of the Monster are stored as words in the elements of H and an extra generator T. It is reasonably quick to calculate the action of one of these words on a vector in V. Using this action, it is possible to perform calculations (such as the order of an element of the Monster). Wilson has exhibited vectors u and v whose joint stabilizer is the trivial group. Thus (for example) one can calculate the order of an element g of the Monster by finding the smallest i > 0 such that giu = u and giv = v.

This and similar constructions (in different characteristics) have been used to prove some interesting properties of the Monster (for example, to find some of its non-local maximal subgroups).

Subgroup structure

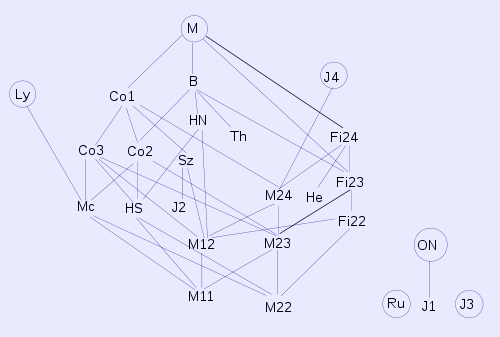
Sporadic Finite Groups Showing (Sporadic) Subgroups (*)

The Monster has at least 43 conjugacy classes of maximal subgroups. Non-abelian simple groups of some 60 isomorphism types are found as subgroups or as quotients of subgroups. The largest alternating group represented is A12. The Monster contains many but not all of the 26 sporadic groups as subgroups. This diagram, based on one in the book Symmetry and the Monster by Mark Ronan, shows how they fit together. The lines signify inclusion, as a subquotient, of the lower group by the upper one. The circled symbols denote groups not involved in larger sporadic groups. For the sake of clarity redundant inclusions are not shown.

Occurrence

The monster can be realized as a Galois group over the rational numbers (Thompson 1984, p. 443), and as a Hurwitz group (Wilson 2004).

Notes

1. ^ Arithmetic groups and the affine E8 Dynkin diagram, by John F. Duncan, in Groups and symmetries: from Neolithic Scots to John McKay
2. ^ le Bruyn, Lieven (22 April 2009), the monster graph and McKay’s observation, http://www.neverendingbooks.org/index.php/the-monster-graph-and-mckays-observation.html

References

* J. H. Conway and S. P. Norton, Monstrous Moonshine, Bull. London Math. Soc. 11 (1979), no. 3, 308—339.
* R. L. Griess, Jr, The Friendly Giant, Inventiones Mathematicae 69 (1982), 1-102
* Conway, J. H.; Curtis, R. T.; Norton, S. P.; Parker, R. A.; and Wilson, R. A.: Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups. Oxford, England 1985.
* S. P. Norton, The uniqueness of the Fischer-Griess Monster, Finite groups---coming of age (Montreal, Que., 1982), 271—285, Contemp. Math., 45, Amer. Math. Soc., Providence, RI, 1985.
* Griess, Robert L., Jr.; Meierfrankenfeld, Ulrich; Segev, Yoav A uniqueness proof for the Monster. Ann. of Math. (2) 130 (1989), no. 3, 567-602.
* Koichiro Harada, Monster, Iwanami Pub. (1999) ISBN 4-000-06055-4, (written in Japanese)
* P. E. Holmes and R. A. Wilson, A computer construction of the Monster using 2-local subgroups, J. London Math. Soc. 67 (2003), 346—364.
* Ivanov, A. A., The Monster Group and Majorana Involutions, Cambridge tracts in mathematics, 176, Cambridege University Press, ISBN 978-0521889940
* S. A. Linton, R. A. Parker, P. G. Walsh and R. A. Wilson, Computer construction of the Monster, J. Group Theory 1 (1998), 307-337.
* M. Ronan, Symmetry and the Monster, Oxford University Press, 2006, ISBN 0192807226 (concise introduction for the lay reader).
* M. du Sautoy, Finding Moonshine, Fourth Estate, 2008, ISBN 978-0-00-721461-7 (another introduction for the lay reader; published in the US by HarperCollins as Symmetry, ISBN 978-0060789404).
* Thompson, John G. (1984), "Some finite groups which appear as Gal L/K, where K ⊆ Q(μn)", Journal of Algebra 89 (2): 437–499, doi:10.1016/0021-8693(84)90228-X, MR751155 .
* Wilson, Robert A. (2001), "The Monster is a Hurwitz group", Journal of Group Theory 4 (4): 367–374, doi:10.1515/jgth.2001.027, MR1859175, http://web.mat.bham.ac.uk/R.A.Wilson/pubs/MHurwitz.ps edit

External links

* MathWorld: Monster Group
* Atlas of Finite Group Representations: Monster group