Wythoff symbol

In geometry, the Wythoff symbol was first used by Coxeter, Longuet-Higgins and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles.

A Schwarz triangle is a triangle that, with its own reflections in its edges, covers the sphere or the plane a finite number of times. The usual representation for the triangle is three numbers – integers or fractions – such that π/x is the angle at one vertex. For example, the triangle (2 3 4) represents the symmetry of a cube, while (5/2 5/2 5/2) is the face of an icosahedron.

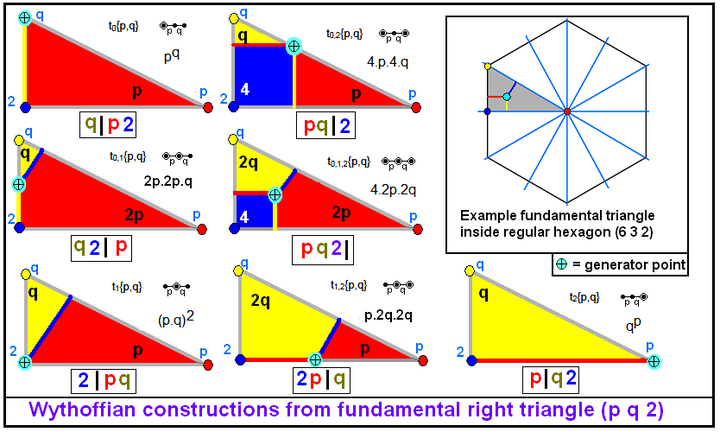
Wythoff's construction in three dimensions consists of choosing a point in the triangle whose distance from each of the sides, if nonzero, is equal, and dropping perpendiculars to each of the edges.

Each edge of the triangle is named for the opposite angle; thus an edge opposite a right angle is designated '2'. The symbol then corresponds to a representation of off | on. Each of the numbers p in the symbol becomes a polygon pn, where n is the number of other edges that appear before the bar. So in 3 | 4 2 the vertex – a point, being here a degenerate polygon with 3×0 sides – lies on the π/3 corner of the triangle, and the altitude from that corner can be considered as forming half of the boundary between a square (having 4×1 sides) and a digon (having 2×1 sides) of zero area.

The special case of the snub figures is done by using the symbol | p q r, which would normally put the vertex at the centre of the sphere. The faces of a snub alternate as p 3 q 3 r 3. This gives an antiprism when q=r=2.

Each symbol represents one uniform polyhedron or tiling, although the same tiling/polyhedron can have different Wythoff symbols from different symmetry generators. For example, the regular cube can be represented by 3 | 4 2 with Oh symmetry, and 2 4 | 2 as a square prism with 2 colors and D4h symmetry, as well as 2 2 2 | with 3 colors and D2h symmetry.

It can be applied with a slight extension to all uniform polyhedra, but the construction methods do not lead to all uniform tilings in euclidean or hyperbolic space.

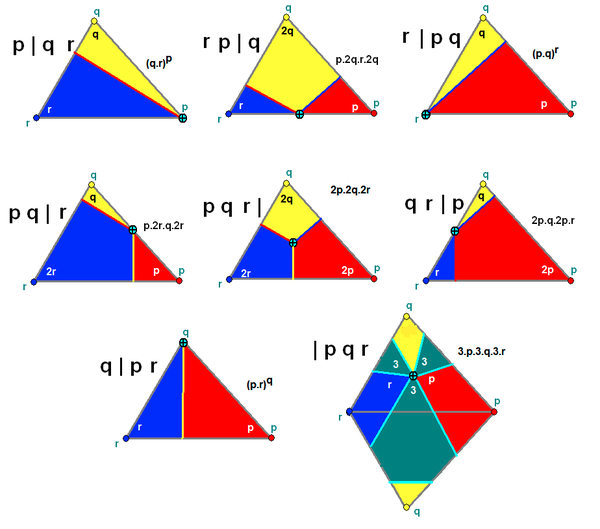
The eight forms for the Wythoff constructions from a general triangle (p q r).

Summary table

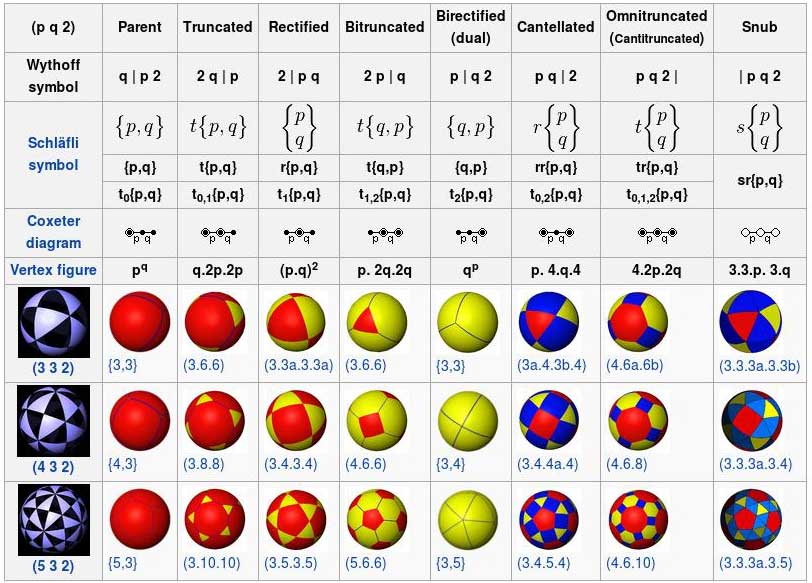
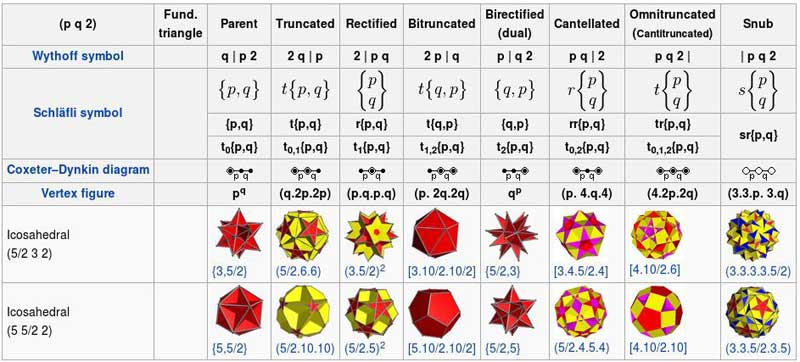
There are seven generator points with each set of p,q,r (and a few special forms):

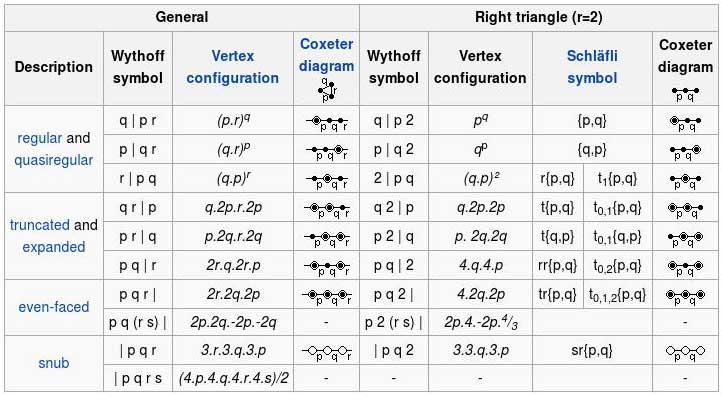
There are three special cases:

Description

The numbers p,q,r describe the fundamental triangle of the symmetry group: at its vertices, the generating mirrors meet in angles of π/p, π/q, π/r. On the sphere there are 3 main symmetry types: (3 3 2), (4 3 2), (5 3 2), and one infinite family (p 2 2), for any p. (All simple families have one right angle and so r=2.)

The position of the vertical bar in the symbol specifies a categorical position of the generator point within the fundamental triangle. The generator point can either be on or off each mirror, activated or not. This distinction creates 8 (2³) possible forms, neglecting one where the generator point is on all the mirrors.

In this notation the mirrors are labeled by the reflection-order of the opposite vertex. The p,q,r values are listed before the bar if the corresponding mirror is active.

The one impossible symbol | p q r implies the generator point is on all mirrors, which is only possible if the triangle is degenerate, reduced to a point. This unused symbol is therefore arbitrarily reassigned to represent the case where all mirrors are active, but odd-numbered reflected images are ignored. The resulting figure has rotational symmetry only.

This symbol is functionally similar to the more general Coxeter-Dynkin diagram, in which each node represents a mirror and the arcs between them – marked with numbers – the angles between the mirrors. (An arc representing a right angle is omitted.) A node is circled if the generator point is not on the mirror.
Symmetry triangles

There are 4 symmetry classes of reflection on the sphere, and two in the Euclidean plane. A few of the infinitely many such patterns in the hyperbolic plane are also listed. (Increasing any of the numbers defining a hyperbolic or Euclidean tiling makes another hyperbolic tiling.)

Point groups:

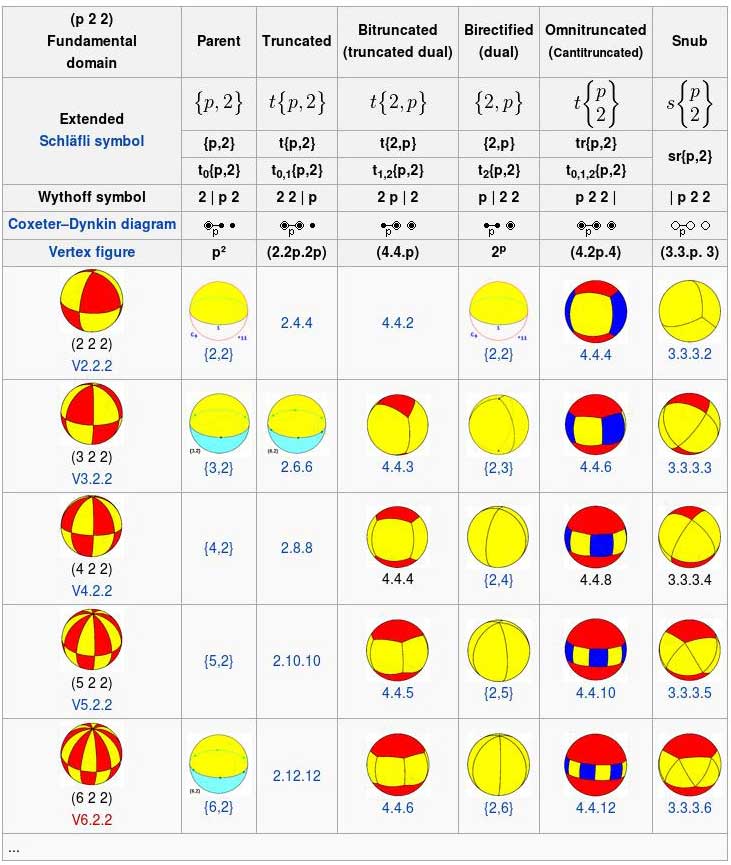
(p 2 2) dihedral symmetry, p = 2, 3, 4... (order 4p)
(3 3 2) tetrahedral symmetry (order 24)
(4 3 2) octahedral symmetry (order 48)
(5 3 2) icosahedral symmetry (order 120)

Euclidean (affine) groups:

(4 4 2) *442 symmetry: 45°-45°-90° triangle
(6 3 2) *632 symmetry: 30°-60°-90° triangle
(3 3 3) *333 symmetry (60°-60°-60° plane)

Hyperbolic groups:

(7 3 2) *732 symmetry
(8 3 2) *832 symmetry
(4 3 3) *433 symmetry
(4 4 3) *443 symmetry
(4 4 4) *444 symmetry
(5 4 2) *542 symmetry
(6 4 2) *642 symmetry

The above symmetry groups only includes the integer solutions on the sphere. The list of Schwarz triangles includes rational numbers, and determine the full set of solutions of nonconvex uniform polyhedra.

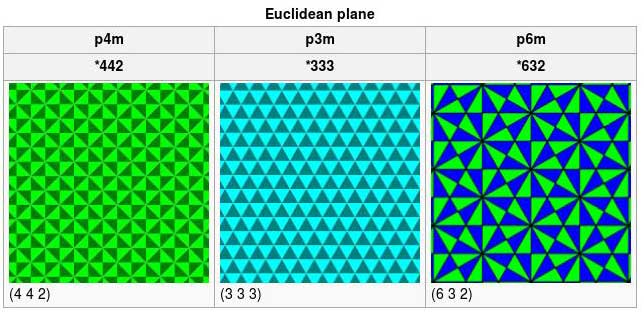
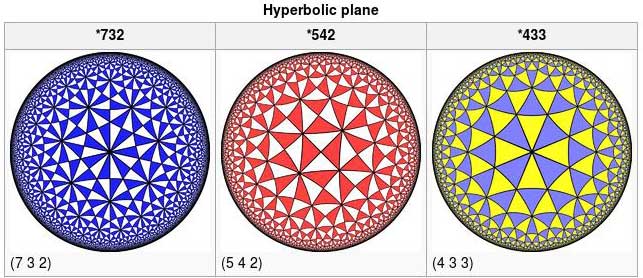
In the tilings above, each triangle is a fundamental domain, colored by even and odd reflections.

Summary spherical, Euclidean and hyperbolic tilings

Selected tilings created by the Wythoff construction are given below.
Spherical tilings (r = 2)

Some overlapping spherical tilings (r = 2)

For a more complete list, including cases where r ≠ 2, see List of uniform polyhedra by Schwarz triangle.

Tilings are shown as polyhedra. Some of the forms are degenerate, given with brackets for vertex figures, with overlapping edges or verices.

Dihedral symmetry (q = r = 2)

Spherical tilings with dihedral symmetry exist for all p = 2, 3, 4, ... many with digon faces which become degenerate polyhedra. Two of the eight forms (Rectified and cantellated) are replications and are skipped in the table.

Euclidean and hyperbolic tilings (r = 2)

Some representative hyperbolic tilings are given, and shown as a Poincaré disk projection.

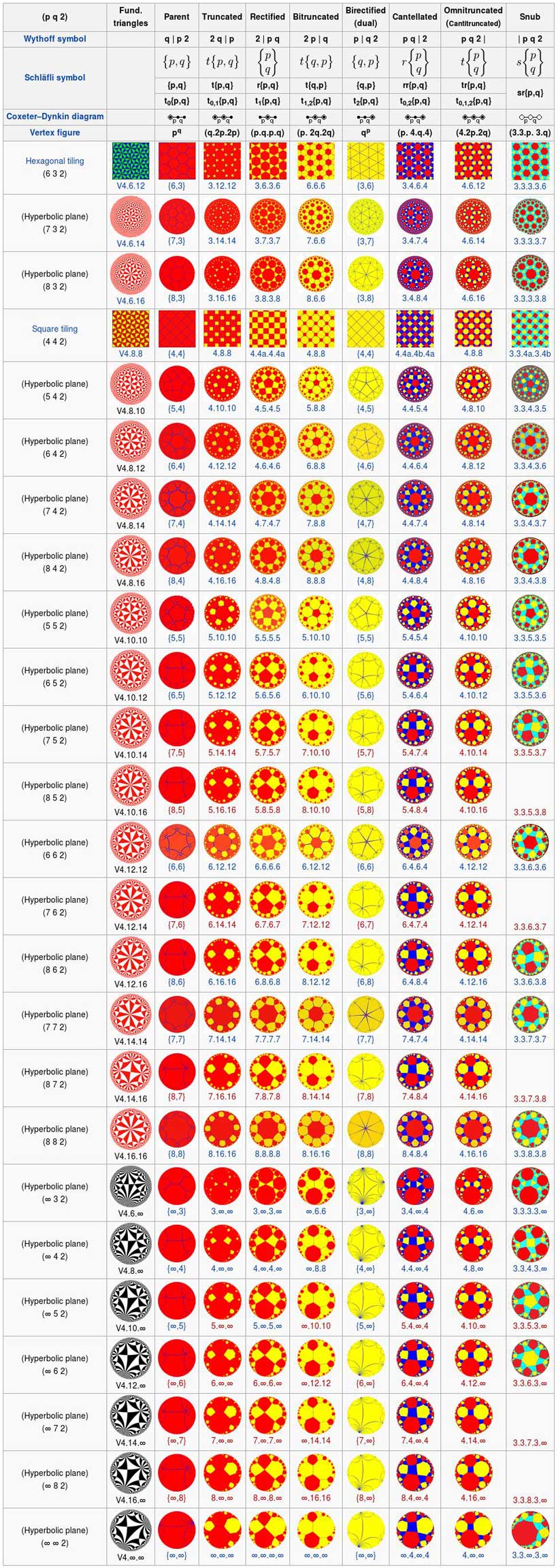
Euclidean and hyperbolic tilings (r > 2)

The Coxeter–Dynkin diagram is given in a linear form, although it is actually a triangle, with the trailing segment r connecting to the first node.