Primorial

For n ≥ 2, the primorial (n#) is the product of all prime numbers less than or equal to n. For example, 7# = 210 is a primorial which is the product of the first four primes multiplied together (2·3·5·7). The name is attributed to Harvey Dubner and is a portmanteau of prime and factorial. The first few primorials are:

2, 6, 30, 210, 2310, 30030, 510510, 9699690, 223092870, 6469693230, 200560490130, 7420738134810, 304250263527210, 13082761331670030, 614889782588491410, ... (sequence A002110 in OEIS)

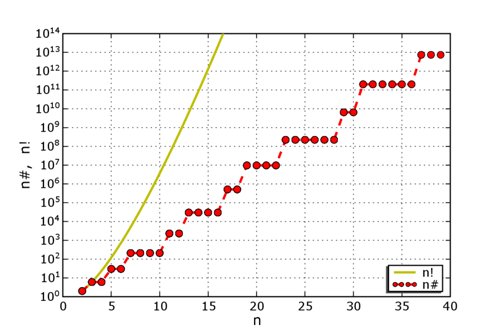
n# as a function of n (red dots), compared to n!. Both plots are logarithmic.

Notation varies; it's common to see pn#, indicating the product of the primes less than or equal to the nth prime (in other words, the product of the first n primes), and also a(n) = pn#. Asymptotically, primorials grow according to:

where "exp" is the exponential function ex and "o" is the "little-o" notation (see Big O notation).[1] Its natural logarithm is the first Chebyshev function, written θ(n) or , which approaches the linear n for large n.[2]

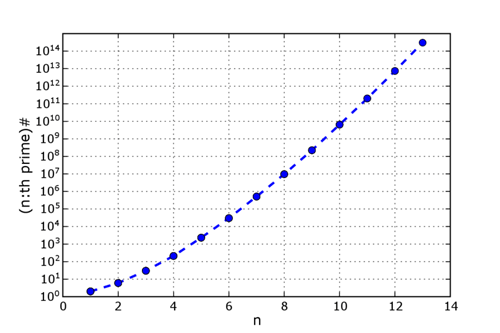
pn# as a function of n, plotted logarithmically.

The idea of multiplying all primes occurs in a proof of the infinitude of the prime numbers; it is applied to show a contradiction in the idea that the primes could be finite in number.

Primorials play a role in the search for prime numbers in additive arithmetic progressions. For instance, 2236133941 + 23# results in a prime, beginning a sequence of thirteen primes found by repeatedly adding 23#, and ending with 5136341251. 23# is also the common difference in arithmetic progressions of fifteen and sixteen primes.

Every highly composite number is a product of primorials (e.g. 360 = 2·6·30).

Primorials are all square-free integers, and each one has more distinct prime factors than any number smaller than it. For each primorial n, the fraction φ(n) / n is smaller than for any lesser integer, where φ is the Euler totient function.

Any completely multiplicative function is defined by its values at primorials, since it is defined by its values at primes, which can be recovered by division of adjacent values.

Table of primorials