| == |
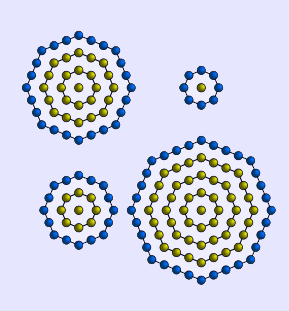
A centered octagonal number is a centered figurate number that represents an octagon with a dot in the center and all other dots surrounding the center dot in successive octagonal layers. The centered octagonal number for n is given by the formula 8Tn − 1 + 1 where T is a regular triangular number, or much more simply, by squaring the odd numbers: (2n + 1)2. The first few centered octagonal numbers are 1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089 All centered octagonal numbers are odd, and in base 10 one can notice the one's digits follow the pattern 1-9-5-9-1. Calculating Ramanujan's tau function on a centered octagonal number yields an odd number, whereas for any other number the function yields an even number. See also regular octagonal number. Retrieved from "http://en.wikipedia.org/" |
|