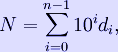Keith number

In mathematics, a Keith number or repfigit number (short for repetitive Fibonacci-like digit) is an integer N > 9 that appears as a term in a linear recurrence relation with initial terms based on its own digits. Given an n-digit number

a sequence SN is formed with initial terms d_n-1, d_n-2, ..., d₁, d₀ and with a general term produced as the sum of the previous n terms. If the number N appears in the sequence SN, then N is said to be a Keith number.

For example, taking 197 in such a way creates the sequence 1, 9, 7, 17, 33, 57, 107, 197,... The first few Keith numbers are:

14, 19, 28, 47, 61, 75, 197, 742, 1104, 1537, 2208, 2580, 3684, 4788, 7385, 7647, 7909 (sequence A007629 in OEIS)

Whether or not there are infinitely many Keith numbers is currently a matter of speculation. There are only 71 Keith numbers below 1019, making them much rarer than prime numbers.

Mike Keith is a mathematician who published a paper on these numbers titled "Repfigit Numbers" in a 1987 issue of the Journal of Recreational Mathematics.

Links

* Keith Number - From MathWorld