.
Monkey saddle
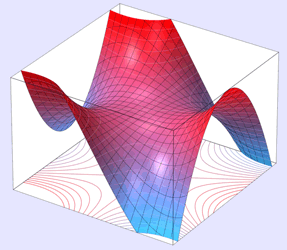
The monkey saddle
In mathematics, the monkey saddle is the surface defined by the equation
![]()
It belongs to the class of saddle surfaces and its name derives from the observation that a saddle for a monkey requires three depressions: two for the legs, and one for the tail. The origin of the monkey saddle is an example of a degenerate critical point.
To see that the monkey saddle has three depressions, let us write the equation for z using complex numbers as
![]() .
.
It follows that z(tx,ty) = t³ z(x,y) for t ≥ 0, so the surface is determined by z on the unit circle. Parametrizing this by eiφ, with φ ∈ [0, 2π), we see that on the unit circle, z(φ) = cos 3φ, so z has three depressions. Replacing 3 with any integer k ≥ 1 we can create a saddle with k depressions.
The term horse saddle is used, in contrast to monkey saddle, to designate a saddle point that is a minimax, that is to say a local minimum or maximum depending on the intersecting plane used. The monkey saddle will have a local maximum along certain planes, but it won't be a local minimum along others — just a point of inflection.
The monkey saddle has an isolated umbilic point with zero Gaussian curvature at the origin, away from the origin the curvature is negative.
See also
* Saddle point
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

