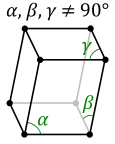
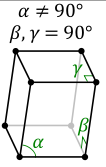
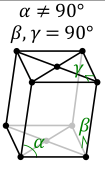
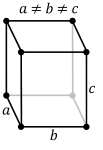
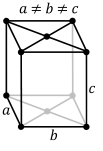
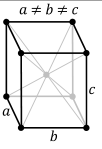
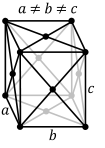
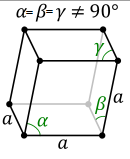
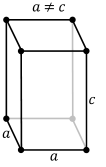
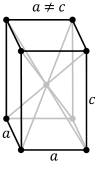
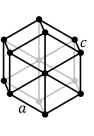
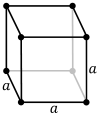
In crystallography, a crystal system or crystal family or lattice system is one of several classes of space groups, lattices, point groups, or crystals. Informally, two crystals tend to be in the same crystal system if they have similar symmetries, though there are many exceptions to this. Crystal systems, crystal families, and lattice systems are similar but slightly different, and there is widespread confusion between them: in particular the trigonal crystal system is often confused with the rhombohedral lattice system, and the term "crystal system" is sometimes used to mean "lattice system" or "crystal family". Space groups and crystals are divided into 7 crystal systems according to their point groups, and into 7 lattice systems according to their Bravais lattices. Five of the crystal systems are essentially the same as five of the lattice systems, but the hexagonal and trigonal crystal systems differ from the hexagonal and rhombohedral lattice systems. The six crystal families are formed by combining the hexagonal and trigonal crystal systems into one hexagonal family, in order to eliminate this confusion.
A lattice system is a class of lattices with the same point group. In three dimensions there are seven lattice systems: triclinic, monoclinic, orthorhombic, tetragonal, rhombohedral, hexagonal, and cubic. The lattice system of a crystal or space group is determined by its lattice but not always by its point group. A crystal system is a class of point groups. Two point groups are placed in the same crystal system if the sets of possible lattice systems of their space groups are the same. For many point groups there is only one possible lattice system, and in these cases the crystal system corresponds to a lattice system and is given the same name. However, for the five point groups in the trigonal crystal class there are two possible lattice systems for their point groups: rhombohedral or hexagonal. In three dimensions there are seven crystal systems: triclinic, monoclinic, orthorhombic, tetragonal, trigonal, hexagonal, and cubic. The crystal system of a crystal or space group is determined by its point group but not always by its lattice. A crystal family also consists of point groups and is formed by combining crystal systems whenever two crystal systems have space groups with the same lattice. In three dimensions a crystal family is almost the same as a crystal system (or lattice system), except that the hexagonal and trigonal crystal systems are combined into one hexagonal family. In three dimensions there are six crystal families: triclinic, monoclinic, orthorhombic, tetragonal, hexagonal, and cubic. The crystal family of a crystal or space group is determined by either its point group or its lattice, and crystal families are the smallest collections of point groups with this property. In dimensions less than three there is no essential difference between crystal systems, crystal families, and lattice systems. There are 1 in dimension 0, 1 in dimension 1, and 4 in dimension 2, called oblique, rectangular, square, and hexagonal. The relation between three-dimensional crystal families, crystal systems, and lattice systems is shown in the following table:
Crystal systems The distribution of the 32 point groups into the 7 crystal systems is given in the following table.
The crystal structures of biological molecules (such as protein structures) can only occur in the 11 enantiomorphic point groups, as biological molecules are invariably chiral. The protein assemblies themselves may have symmetries other than those given above, because they are not intrinsically restricted by the Crystallographic restriction theorem. For example the Rad52 DNA binding protein has an 11-fold rotational symmetry (in human), however, it must form crystals in one of the 11 enantiomorphic point groups given above. Lattice systems The distribution of the 14 Bravais lattice types into 7 lattice systems is given in the following table.
Such symmetry groups consist of translations by vectors of the form
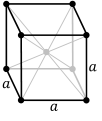
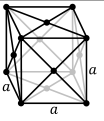
where n1, n2, and n3 are integers and a1, a2, and a3 are three non-coplanar vectors, called primitive vectors. These lattices are classified by space group of the translation lattice itself; there are 14 Bravais lattices in three dimensions; each can apply in one lattice system only. They represent the maximum symmetry a structure with the translational symmetry concerned can have. All crystalline materials must, by definition fit in one of these arrangements (not including quasicrystals). For convenience a Bravais lattice is depicted by a unit cell which is a factor 1, 2, 3 or 4 larger than the primitive cell. Depending on the symmetry of a crystal or other pattern, the fundamental domain is again smaller, up to a factor 48. The Bravais lattices were studied by Moritz Ludwig Frankenheim (1801-1869), in 1842, who found that there were 15 Bravais lattices. This was corrected to 14 by A. Bravais in 1848. See also * Crystal structure
* Hahn, Theo, ed. (2002), International Tables for Crystallography, Volume A: Space Group Symmetry, A (5th ed.), Berlin, New York: Springer-Verlag, doi:10.1107/97809553602060000100, ISBN 978-0-7923-6590-7, http://it.iucr.org/A/
* Overview of the 32 groups Retrieved from "http://en.wikipedia.org/" |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||