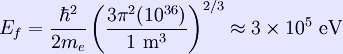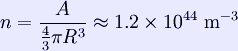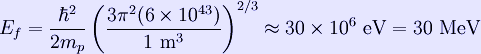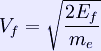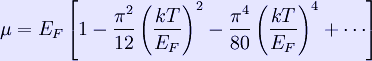The Fermi energy is a concept in quantum mechanics referring to the energy of the highest occupied quantum state in a system of fermions at absolute zero temperature. This article requires a basic knowledge of quantum mechanics.

Introduction

Context

In quantum mechanics, a group of particles known as fermions (for example, electrons, protons and neutrons are fermions) obey the Pauli exclusion principle. This principle states that two identical fermions can not be in the same quantum state. The states are labeled by a set of quantum numbers. In a system containing many fermions (like electrons in a metal) each fermion will have a different set of quantum numbers. To determine the lowest energy a system of fermions can have, we first group the states in sets with equal energy and order these sets by increasing energy. Starting with an empty system, we then add particles one at a time, consecutively filling up the unoccupied quantum states with lowest-energy. When all the particles have been put in, the Fermi energy is the energy of the highest occupied state. What this means is that even if we have extracted all possible energy from a metal by cooling it down to near absolute zero temperature (0 kelvins), the electrons in the metal are still moving around, the fastest ones would be moving at a velocity that corresponds to a kinetic energy equal to the Fermi energy. This is the Fermi velocity. The Fermi energy is one of the important concepts of condensed matter physics. It is used, for example, to describe metals, insulators, and semiconductors. It is a very important quantity in the physics of superconductors, in the physics of quantum liquids like low temperature helium (both normal 3He and superfluid 4He), and it is quite important to nuclear physics and to understand the stability of white dwarf stars against gravitational collapse.

Advanced context

The Fermi energy (EF) of a system of non-interacting fermions is the increase in the ground state energy when exactly one particle is added to the system. It can also be interpreted as the maximum energy of an individual fermion in this ground state. The chemical potential at zero temperature is equal to the Fermi energy.

Illustration of the concept for a one dimensional square well

The one dimensional infinite square well is a model for a one dimensional box. It is a standard model-system in quantum mechanics for which the solution for a single particle is well known. The levels are labeled by a single quantum number n and the energies are given by

Suppose now that instead of one particle in this box we have N particles in the box and that these particles are fermions with spin 1/2. Then only two particles can have the same energy i.e. two particles can have the energy of , or two particles can have energy E2 = 4E1 and so forth. The reason that two particles can have the same energy is that a spin-1/2 particle can have a spin of 1/2 (spin up) or a spin of -1/2 (spin down), leading to two states for each energy level. When we look at the total energy of this system, the configuration for which the total energy is lowest (the ground state), is the configuration where all the energy levels up to n=N/2 are occupied and all the higher levels are empty. The Fermi energy is therefore

.

The three-dimensional case

The three-dimensional isotropic case is known as the fermi ball.

Let us now consider a three-dimensional cubical box that has a side length L (see infinite square well). This turns out to be a very good approximation for describing electrons in a metal. The states are now labeled by three quantum numbers nx, ny, and nz. The single particle energies are

,

n_x, n_y, n_z are positive integers.

There are multiple states with the same energy, for example E₁₀₀ = E₀₁₀ = E₀₀1. Now let's put N non-interacting fermions of spin 1/2 into this box. To calculate the Fermi energy, we look at the case for N is large.

If we introduce a vector then each quantum state corresponds to a point in 'n-space' with Energy

The number of states with energy less than Ef is equal to the number of states that lie within a sphere of radius in the region of n-space where nx, ny, nz are positive. In the ground state this number equals the number of fermions in the system.

,

the factor of two is once again because there are two spin states, the factor of 1/8 is because only 1/8 of the sphere lies in the region where all n are positive. We find

so the Fermi energy is given by

Which results in a relationship between the fermi energy and the number of particles per volume (when we replace L2 with V2/3):

,

The total energy of a fermi ball of N0 fermions is given by

f

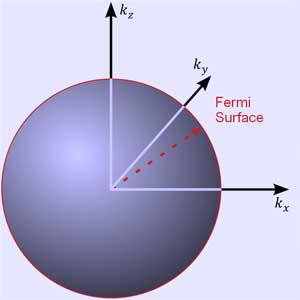
The free fermions that occupy the lowest energy states form a sphere in momentum space. The surface of this sphere is the Fermi surface.

Typical fermi energies

White dwarfs

Stars known as White dwarfs have mass comparable to our Sun, but have a radius about 100 times smaller. The high densities means that the electrons are no longer bound to single nuclei and instead form a degenerate electron gas. The number density of electrons in a White dwarf are on the order of 1036 electrons/m3. This means their fermi energy is:

Nucleus

Another typical example is that of the particles in a nucleus of an atom. The radius of the nucleus is roughly:

where A is the number of nucleons.

The number density of nucleons in a nucleus is therefore:

Now since the fermi energy only applies to fermions of the same type, one must divide this density in two. This is because the presence of neutrons does not affect the fermi energy of the protons in the nucleus, and vice versa.

So the fermi energy of a nucleus is about:

The radius of the nucleus admits deviations around the value mentioned above, so a typical value for the fermi energy usually given is 38 MeV.

Fermi level

The Fermi level is the highest occupied energy level at absolute zero, that is, all energy levels up to the Fermi level are occupied by electrons. Since fermions cannot exist in identical energy states (see the exclusion principle), at absolute zero, electrons pack into the lowest available energy states and build up a "Fermi sea" of electron energy states. [1] In this state (at 0 K), the average energy of an electron is given by:

where Ef is the Fermi energy.

The Fermi momentum is the momentum of fermions at the Fermi surface. The Fermi momentum is given by:

where m_e is the mass of the electron.

This concept is usually applied in the case of dispersion relations between the energy and momentum that do not depend on the direction. In more general cases, one must consider the Fermi energy.

The Fermi velocity is the velocity of fermions at the Fermi surface. It is defined by:

where me is the mass of the electron.

Below the Fermi temperature, a substance gradually expresses more and more quantum effects of cooling. The Fermi temperature is defined by:

where k is the Boltzmann constant.

Quantum mechanics

According to quantum mechanics, fermions -- particles with a half-integer spin, usually 1/2, such as electrons -- follow the Pauli exclusion principle, which states that multiple particles may not occupy the same quantum state. Consequently, fermions obey Fermi-Dirac statistics. The ground state of a non-interacting fermion system is constructed by starting with an empty system and adding particles one at a time, consecutively filling up the lowest-energy unoccupied quantum states. When the desired number of particles has been reached, the Fermi energy is the energy of the highest occupied molecular orbital (HOMO). Within conductive materials, this is equivalent to the lowest unoccupied molecular orbital (LUMO); however, within other materials there will be a significant gap between the HOMO and LUMO on the order of 2-3 eV.

Free electron gas

In the free electron gas, the quantum mechanical version of an ideal gas of fermions, the quantum states can be labeled according to their momentum. Something similar can be done for periodic systems, such as electrons moving in the atomic lattice of a metal, using something called the "quasi-momentum" or "crystal momentum" (see Bloch wave). In either case, the Fermi energy states reside on a surface in momentum space known as the Fermi surface. For the free electron gas, the Fermi surface is the surface of a sphere; for periodic systems, it generally has a contorted shape (see Brillouin zones). The volume enclosed by the Fermi surface defines the number of electrons in the system, and the topology is directly related to the transport properties of metals, such as electrical conductivity. The study of the Fermi surface is sometimes called Fermiology. The Fermi surfaces of most metals are well studied both theoretically and experimentally.

The Fermi energy of the free electron gas is related to the chemical potential by the equation

where EF is the Fermi energy, k is the Boltzmann constant and T is temperature. Hence, the chemical potential is approximately equal to the Fermi energy at temperatures of much less than the characteristic Fermi temperature EF/k. The characteristic temperature is on the order of 105 K for a metal, hence at room temperature (300 K), the Fermi energy and chemical potential are essentially equivalent. This is significant since it is the chemical potential, not the Fermi energy, which appears in Fermi-Dirac statistics.

See also

* fermi gas
* semiconductors
* electrical engineering
* electronics
* thermodynamics

References

* Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2nd ed.). W. H. Freeman Company. ISBN 0-7167-1088-9.
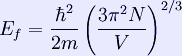* Table of fermi energies, velocities, and temperatures for various elements.
* a discussion of fermi gases and fermi temperatures.