Kondo effect

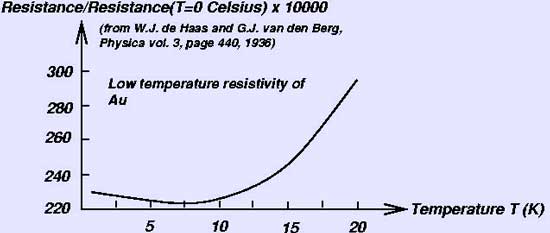
According to the Kondo effect, the electrical resistance will diverge as the temperature approaches 0 K. The temperature dependence of the resistance including the Kondo effect is written as:

where ρ₀ is the residual resistance, aT² shows the contribution from the Fermi liquid properties, and the term bT⁵ is from the lattice vibrations. Jun Kondo has derived the third term of the logarithmic dependence. Later calculations refined this result to produce a finite resistivity but retained the feature of a resistance minimum at a non-zero temperature. One defines the Kondo temperature as the energy scale limiting the validity of the Kondo results. The Anderson model and accompanying renormalization theory was an important contribution to understanding the underlying physics of the problem.

The Kondo effect is the first known example of asymptotic freedom in physics, in which the coupling becomes non-perturbatively strong at low temperatures/low energies. In the Kondo problem, this refers to the interaction between the localized magnetic impurities and the itinerant electrons. In a more complex form, asymptotic freedom underlies the theory of quantum chromodynamics, or the so-called strong nuclear force so that quarks, the fundamental constituents of nuclear matter, interact weakly at high energies and strongly at low energies, preventing the unbinding of baryons (fermions like protons or neutrons with three quarks) or mesons (bosons like pions with two quarks), the composite particles of nuclear matter. For this discovery, Frank Wilczek, David Gross, and David Politzer shared the 2004 Nobel Prize in physics.

Kondo effect: How gold with a small amount of what were probably iron impurities behaves at low temperatures

Extended to a lattice of magnetic impurities, the Kondo effect is believed to underly the formation of heavy fermions in intermetallic compounds based especially upon rare earth elements like cerium, praseodymium, and ytterbium, and actinide elements like uranium. In these materials, the nonperturbative growth of the interaction leads to quasi-electrons with masses up to thousands of times the free electron mass, ie, the electrons are dramatically slowed by the interactions. In a number of instances they actually are superconductors! More recently, it is believed that a manifestation of the Kondo effect is necessary for understanding the unusual metallic delta-phase of plutonium.

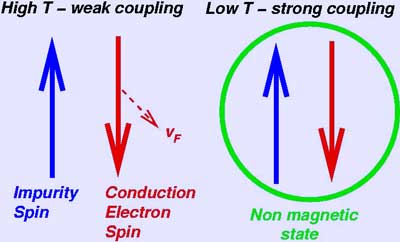
Schematic of the weakly coupled high temperature situation in which the magnetic moments of conduction electrons in the metal host pass by the impurity magnetic moment at speeds of vF, the Fermi velocity, experiencing only a mild antiferromagnetic correlation in the vicinity of the impurity. In contrast, as the temperature tends to zero the impurity magnetic moment and one conduction electron moment bind very strongly to form an overall non-magnetic state.

Links

* Jun Kondo's web page - follow links in English, other parts are written in Japanese
* Kondo Effect - 40 Years after the Discovery - special issue of the Journal of the Physical Society of Japan
* The Kondo Problem to Heavy Fermions - Monograph on the Kondo effect by A.C. Hewson (ISBN 0-521-59947-4)
* Exotic Kondo Effects in Metals - Monograph on newer versions of the Kondo effect in non-magnetic contexts especially (ISBN 0-7484-0889-4)
* Correlated electrons in δ-plutonium within a dynamical mean-field picture, Nature 410, 793 (2001). Nature article exploring the links of the Kondo effect and plutonium
* Kondo effect on arxiv.org