.
Development of Gravity Pendulums in the 19th Century, by Victor Fritz Lenzen and Robert P. Multhauf
SMITHSONIAN INSTITUTION
UNITED STATES NATIONAL MUSEUM
BULLETIN 240
SMITHSONIAN PRESS
MUSEUM OF HISTORY AND TECHNOLOGY
Contributions
From the
Museum
of History and
Technology
Papers 34-44
On Science and Technology
SMITHSONIAN INSTITUTION · WASHINGTON, D.C. 1966
Publications of the United States National Museum
The scholarly and scientific publications of the United States National Museum include two series, Proceedings of the United States National Museum and United States National Museum Bulletin.
In these series, the Museum publishes original articles and monographs dealing with the collections and work of its constituent museums—The Museum of Natural History and the Museum of History and Technology—setting forth newly acquired facts in the fields of anthropology, biology, history, geology, and technology. Copies of each publication are distributed to libraries, to cultural and scientific organizations, and to specialists and others interested in the different subjects.
The Proceedings, begun in 1878, are intended for the publication, in separate form, of shorter papers from the Museum of Natural History. These are gathered in volumes, octavo in size, with the publication date of each paper recorded in the table of contents of the volume.
In the Bulletin series, the first of which was issued in 1875, appear longer, separate publications consisting of monographs (occasionally in several parts) and volumes in which are collected works on related subjects. Bulletins are either octavo or quarto in size, depending on the needs of the presentation. Since 1902 papers relating to the botanical collections of the Museum of Natural History have been published in the Bulletin series under the heading Contributions from the United States National Herbarium, and since 1959, in Bulletins titled “Contributions from the Museum of History and Technology,” have been gathered shorter papers relating to the collections and research of that Museum.
The present collection of Contributions, Papers 34-44, comprises Bulletin 240. Each of these papers has been previously published in separate form. The year of publication is shown on the last page of each paper.
Frank A. Taylor
Director, United States National Museum
Contributions from
The Museum of History and Technology:
Paper 44
Development of Gravity Pendulums in the 19th Century
Victor F. Lenzen and Robert P. Multhauf
GALILEO, HUYGENS, AND NEWTON 304
FIGURE OF THE EARTH 306
EARLY TYPES OF PENDULUMS 309
KATER’S CONVERTIBLE AND INVARIABLE PENDULUMS 314
REPSOLD-BESSEL REVERSIBLE PENDULUM 320
PEIRCE AND DEFFORGES INVARIABLE, REVERSIBLE PENDULUMS 327
VON STERNECK AND MENDENHALL PENDULUMS 331
ABSOLUTE VALUE OF GRAVITY AT POTSDAM 338
APPLICATION OF GRAVITY SURVEYS 342
SUMMARY 346
Victor F. Lenzen and
Robert P. Multhauf
DEVELOPMENT OF GRAVITY PENDULUMS
IN THE 19th CENTURY
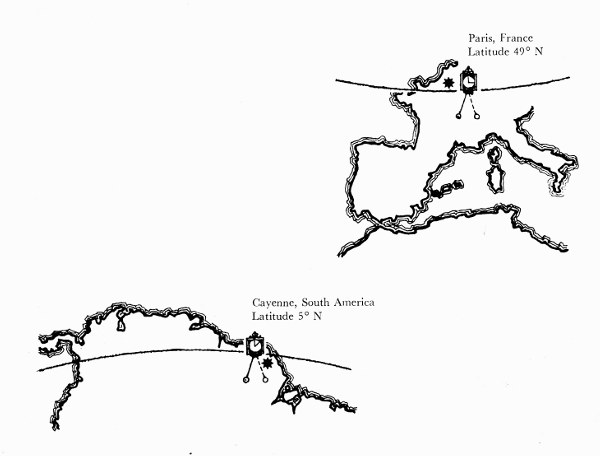
Figure 1.—A study of the figure of the earth was one of the earliest projects of the French Academy of Sciences. In order to test the effect of the earth’s rotation on its gravitational force, the Academy in 1672 sent Jean Richer to the equatorial island of Cayenne to compare the rate of a clock which was known to have kept accurate time in Paris. Richer found that the clock lost 2 minutes and 28 seconds at Cayenne, indicating a substantial decrease in the force of gravity on the pendulum. Subsequent pendulum experiments revealed that the period of a pendulum varied not only with the latitude but also regionally, under the influence of topographical features such as mountains. It became clear that the measurement of gravity should be made a part of the work of the geodetic surveyor.
The history of gravity pendulums dates back to the time of Galileo. After the discovery of the variation of the force of gravity over the surface of the earth, gravity measurement became a major concern of physics and geodesy. This article traces the history of the development of instruments for this purpose.
THE AUTHORS: Victor F. Lenzen is Professor of Physics, Emeritus, at the University of California at Berkeley and Robert P. Multhauf is Chairman of the Department of Science and Technology in the Smithsonian Institution’s Museum of History and Technology.
The intensity of gravity, or the acceleration of a freely falling body, is an important physical quantity for the several physical sciences. The intensity of gravity determines the weight of a standard pound or kilogram as a standard or unit of force. In physical experiments, the force on a body may be measured by determining the weight of a known mass which serves to establish equilibrium against it. Thus, in the absolute determination of the ampere with a current balance, the force between two coils carrying current is balanced by the earth’s gravitational force upon a body of determinable mass. The intensity of gravity enters into determinations of the size of the earth from the angular velocity of the moon, its distance from the earth, and Newton’s inverse square law of gravitation and the laws of motion. Prediction of the motion of an artificial satellite requires an accurate knowledge of gravity for this astronomical problem.
The gravity field of the earth also provides data for a determination of the figure of the earth, or geoid, but for this problem of geodesy relative values of gravity are sufficient. If g is the intensity of gravity at some reference station, and Δg is the difference between intensities at two stations, the values of gravity in geodetic calculations enter as ratios (Δg)/g over the surface of the earth. Gravimetric investigations in conjunction with other forms of geophysical investigation, such as seismology, furnish data to test[Pg 304] hypotheses concerning the internal structure of the earth.
Whether the intensity of gravity is sought in absolute or relative measure, the most widely used instrument for its determination since the creation of classical mechanics has been the pendulum. In recent decades, there have been invented gravity meters based upon the principle of the spring, and these instruments have made possible the rapid determination of relative values of gravity to a high degree of accuracy. The gravity meter, however, must be calibrated at stations where the absolute value of gravity has been determined by other means if absolute values are sought. For absolute determinations of gravity, the pendulum historically has been the principal instrument employed. Although alternative methods of determining absolute values of gravity are now in use, the pendulum retains its value for absolute determinations, and even retains it for relative determinations, as is exemplified by the Cambridge Pendulum Apparatus and that of the Dominion Observatory at Ottawa, Ontario.
The pendulums employed for absolute or relative determinations of gravity have been of two basic types. The first form of pendulum used as a physical instrument consisted of a weight suspended by a fiber, cord, or fine wire, the upper end of which was attached to a fixed support. Such a pendulum may be called a “simple” pendulum; the enclosure of the word simple by quotation marks is to indicate that such a pendulum is an approximation to a simple, or mathematical pendulum, a conceptual object which consists of a mass-point suspended by a weightless inextensible cord. If l is the length of the simple pendulum, the time of swing (half-period in the sense of physics) for vibrations of infinitely small amplitude, as derived from Newton’s laws of motion and the hypothesis that weight is proportional to mass, is T = π√(l/g).
The second form of pendulum is the compound, or physical, pendulum. It consists of an extended solid body which vibrates about a fixed axis under the action of the weight of the body. A compound pendulum may be constituted to oscillate about one axis only, in which case it is nonreversible and applicable only for relative measurements. Or a compound pendulum may be constituted to oscillate about two axes, in which case it is reversible (or “convertible”) and may be used to determine absolute values of gravity. Capt. Henry Kater, F.R.S., during the years 1817-1818 was the first to design, construct, and use a compound pendulum for the absolute determination of gravity. He constructed a convertible pendulum with two knife edges and with it determined the absolute value of gravity at the house of Henry Browne, F.R.S., in Portland Place, London. He then constructed a similar compound pendulum with only one knife edge, and swung it to determine relative values of gravity at a number of stations in the British Isles. The 19th century witnessed the development of the theory and practice of observations with pendulums for the determination of absolute and relative values of gravity.
Galileo, Huygens, and Newton
The pendulum has been both an objective and an instrument of physical investigation since the foundations of classical mechanics were fashioned in the 17th century.[1] It is tradition that the youthful Galileo discovered that the period of oscillation of a pendulum is constant by observations of the swings of the great lamp suspended from the ceiling in the cathedral of Pisa.[2] The lamp was only a rough approximation to a simple pendulum, but Galileo later performed more accurate experiments with a “simple” pendulum which consisted of a heavy ball suspended by a cord. In an experiment designed to confirm his laws of falling bodies, Galileo lifted the ball to the level of a given altitude and released it. The ball ascended to the same level on the other side of the vertical equilibrium position and thereby confirmed a prediction from the laws. Galileo also discovered that the period of vibration of a “simple” pendulum varies as the square root of its length, a[Pg 305] result which is expressed by the formula for the time of swing of the ideal simple pendulum. He also used a pendulum to measure lapse of time, and he designed a pendulum clock. Galileo’s experimental results are important historically, but have required correction in the light of subsequent measurements of greater precision.
Mersenne in 1644 made the first determination of the length of the seconds pendulum,[3] that is, the length of a simple pendulum that beats seconds (half-period in the sense of physics). Subsequently, he proposed the problem to determine the length of the simple pendulum equivalent in period to a given compound pendulum. This problem was solved by Huygens, who in his famous work Horologium oscillatorium ... (1673) set forth the theory of the compound pendulum.[4]
Huygens derived a theorem which has provided the basis for the employment of the reversible compound pendulum for the absolute determination of the intensity of gravity. The theorem is that a given compound pendulum possesses conjugate points on opposite sides of the center of gravity; about these points, the periods of oscillation are the same. For each of these points as center of suspension the other point is the center of oscillation, and the distance between them is the length of the equivalent simple pendulum. Earlier, in 1657, Huygens independently had invented and patented the pendulum clock, which rapidly came into use for the measurement of time. Huygens also created the theory of centripetal force which made it possible to calculate the effect of the rotation of the earth upon the observed value of gravity.
The theory of the gravity field of the earth was founded upon the laws of motion and the law of gravitation by Isaac Newton in his famous Principia (1687). It follows from the Newtonian theory of gravitation that the acceleration of gravity as determined on the surface of the earth is the resultant of two factors: the principal factor is the gravitational attraction of the earth upon bodies, and the subsidiary factor is the effect of the rotation of the earth. A body at rest on the surface of the earth requires some of the gravitational attraction for the centripetal acceleration of the body as it is carried in a circle with constant speed by the rotation of the earth about its axis. If the rotating earth is used as a frame of reference, the effect of the rotation is expressed as a centrifugal force which acts to diminish the observed intensity of gravity.
Glossary of Gravity Terminology
ABSOLUTE GRAVITY: the value of the acceleration of gravity, also expressed by the length of the seconds pendulum.
RELATIVE GRAVITY: the value of the acceleration of gravity relative to the value at some standard point.
SIMPLE PENDULUM: see theoretical pendulum.
THEORETICAL PENDULUM: a heavy bob (point-mass) at the end of a weightless rod.
SECONDS PENDULUM: a theoretical or simple pendulum of such length that its time of swing (half-period) is one second. (This length is about one meter.)
GRAVITY PENDULUM: a precisely made pendulum used for the measurement of gravity.
COMPOUND PENDULUM: a pendulum in which the supporting rod is not weightless; in other words, any actual pendulum.
CONVERTIBLE PENDULUM: a compound pendulum having knife edges at different distances from the center of gravity. Huygens demonstrated (1673) that if such a pendulum were to swing with equal periods from either knife edge, the distance between those knife edges would be equal to the length of a theoretical or simple pendulum of the same period.
REVERSIBLE PENDULUM: a convertible pendulum which is also symmetrical in form.
INVARIABLE PENDULUM: a compound pendulum with only one knife edge, used for relative measurement of gravity.
From Newton’s laws of motion and the hypothesis that weight is proportional to mass, the formula for the half-period of a simple pendulum is given by T = π√(l/g). If a simple pendulum beats seconds, 1 = π√(λ/g), where λ is the length of the seconds pendulum. From T = π√(l/g) and 1 = π√(λ/g), it follows that λ = l/T2. Then g = π2λ. Thus, the intensity of gravity can be expressed in terms of the length of the seconds pendulum, as well as by the acceleration of a freely falling body. During the 19th century, gravity usually was expressed in terms of the length of the seconds pendulum, but present practice is to express gravity in terms of g, for which the unit is the gal, or one centimeter per second per second.[Pg 306]

Figure 2.—This drawing, from Richer’s Observations astronomiques et physiques faites en l’isle de Caïenne (Paris, 1679), shows most of the astronomical instruments used by Richer, namely, one of the two pendulum clocks made by Thuret, the 20-foot and the 5-foot telescopes and the large quadrant. The figure may be intended as a portrait of Richer. This drawing was done by Sebastian Le Clerc, a young illustrator who made many illustrations of the early work of the Paris Academy.
Figure of the Earth
A principal contribution of the pendulum as a physical instrument has been the determination of the figure of the earth.[5] That the earth is spherical in form was accepted doctrine among the ancient Greeks. Pythagoras is said to have been the first to describe the earth as a sphere, and this view was adopted by Eudoxus and Aristotle.
The Alexandrian scientist Eratosthenes made the first estimate of the diameter and circumference of a supposedly spherical earth by an astronomical-geodetic method. He measured the angle between the directions of the rays of the sun at Alexandria and Syene (Aswan), Egypt, and estimated the distance between these places from the length of time required by a caravan of camels to travel between them. From the central angle corresponding to the arc on the surface, he calculated the radius and hence the circumference of the earth. A second measurement was undertaken by Posidonius, who measured the altitudes of stars at Alexandria and Rhodes and estimated the distance between them from the time required to sail from one place to the other.
With the decline of classical antiquity, the doctrine of the spherical shape of the earth was lost, and only one investigation, that by the Arabs under Calif Al-Mamun in A.D. 827, is recorded until the 16th century. In 1525, the French mathematician Fernel measured the length of a degree of latitude between Paris and Amiens by the revolutions of the wheels of his carriage, the circumference of which he had determined. In England, Norwood in 1635 measured the length of an arc between London and York with a chain. An important forward step in geodesy was the measurement of distance by triangulation, first by Tycho Brahe, in Denmark, and later, in 1615, by Willebrord Snell, in Holland.
Of historic importance, was the use of telescopes in the triangulation for the measurement of a degree of arc by the Abbé Jean Picard in 1669.[6] He had been commissioned by the newly established Academy of Sciences to measure an arc corresponding to an angle of 1°, 22′, 55″ of the meridian between Amiens and Malvoisine, near Paris. Picard proposed to the Academy the measurement of the meridian of Paris through all of France, and this project was supported by Colbert, who obtained the approval of the King. In 1684, Giovanni-Domenico Cassini and De la Hire commenced a trigonometrical measure of an arc south of Paris; subsequently, Jacques Cassini, the son[Pg 307] of Giovanni-Domenico, added the arc to the north of Paris. The project was completed in 1718. The length of a degree of arc south of Paris was found to be greater than the length north of Paris. From the difference, 57,097 toises[7] minus 56,960 toises, it was concluded that the polar diameter of the earth is larger than the equatorial diameter, i.e., that the earth is a prolate spheroid (fig. 3).
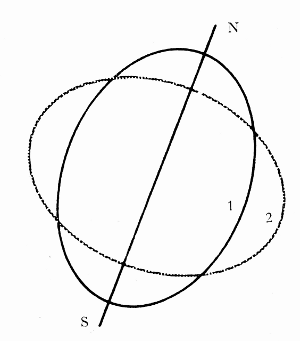
Figure 3.—Measurements of the length of a degree of latitude which were completed in different parts of France in 1669 and 1718 gave differing results which suggested that the shape of the earth is not a sphere but a prolate spheroid (1). But Richer’s pendulum observation of 1672, as explained by Huygens and Newton, indicated that its shape is that of an oblate spheroid (2). The disagreement is reflected in this drawing. In the 1730’s it was resolved in favor of the latter view by two French geodetic expeditions for the measurement of degrees of latitude in the equatorial and polar regions (Ecuador—then part of Peru—and Lapland).
Meanwhile, Richer in 1672 had been sent to Cayenne, French Guiana, to make astronomical observations and to measure the length of the seconds pendulum.[8] He took with him a pendulum clock which had been adjusted to keep accurate time in Paris. At Cayenne, however, Richer found that the clock was retarded by 2 minutes and 28 seconds per day (fig. 1). He also fitted up a “simple” pendulum to vibrate in seconds and measured the length of this seconds pendulum several times every week for 10 months. Upon his return to Paris, he found that the length of the “simple” pendulum which beat seconds at Cayenne was 1-1/4 Paris lines[9] shorter than the length of the seconds pendulum at Paris. Huygens explained the reduction in the length of the seconds pendulum—and, therefore, the lesser intensity of gravity at the equator with respect to the value at Paris—in terms of his theory of centripetal force as applied to the rotation of the earth and pendulum.[10]
A more complete theory was given by Newton in the Principia.[11] Newton showed that if the earth is assumed to be a homogeneous, mutually gravitating fluid globe, its rotation will result in a bulging at the equator. The earth will then have the form of an oblate spheroid, and the intensity of gravity as a form of universal gravitation will vary with position on the surface of the earth. Newton took into account gravitational attraction and centrifugal action, and he calculated the ratio of the axes of the spheroid to be 230:229. He calculated and prepared a table of the lengths of a degree of latitude and of the seconds pendulum for every 5° of latitude from the equator to the pole. A discrepancy between his predicted length of the seconds pendulum at the equator and Richer’s measured length was explained by Newton in terms of the expansion of the scale with higher temperatures near the equator.
Newton’s theory that the earth is an oblate spheroid was confirmed by the measurements of Richer, but was rejected by the Paris Academy of Sciences, for it contradicted the results of the Cassinis, father and son, whose measurements of arcs to the south and north of Paris had led to the conclusion that the earth is a prolate spheroid. Thus, a controversy arose between the English scientists and the Paris Academy. The conflict was finally resolved by the results of expeditions sent by the Academy to Peru and Sweden. The first expedition, under Bouguer, La Condamine, and Godin in 1735, went to a region[Pg 308] in Peru, and, with the help of the Spaniard Ullo, measured a meridian arc of about 3°7′ near Quito, now in Ecuador.[12] The second expedition, with Maupertuis and Clairaut in 1736, went to Lapland within the Arctic Circle and measured an arc of about 1° in length.[13] The northern arc of 1° was found to be longer than the Peruvian arc of 1°, and thus it was confirmed that the earth is an oblate spheroid, that is, flattened at the poles, as predicted by the theory of Newton.
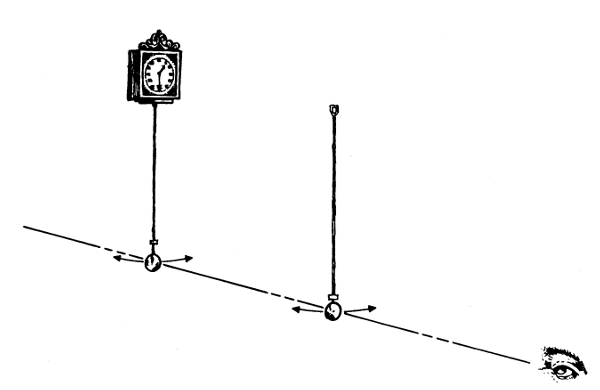
Figure 4.—The direct use of a clock to measure the force of gravity was found to be limited in accuracy by the necessary mechanical connection of the pendulum to the clock, and by the unavoidable difference between the characteristics of a clock pendulum and those of a theoretical (usually called “simple”) pendulum, in which the mass is concentrated in the bob, and the supporting rod is weightless.
After 1735, the clock was used only to time the swing of a detached pendulum, by the method of “coincidences.” In this method, invented by J. J. Mairan, the length of the detached pendulum is first accurately measured, and the clock is corrected by astronomical observation. The detached pendulum is then swung before the clock pendulum as shown here. The two pendulums swing more or less out of phase, coming into coincidence each time one has gained a vibration. By counting the number of coincidences over several hours, the period of the detached pendulum can be very accurately determined. The length and period of the detached pendulum are the data required for the calculation of the force of gravity.
The period from Eratosthenes to Picard has been called the spherical era of geodesy; the period from Picard to the end of the 19th century has been called the ellipsoidal period. During the latter period the earth was conceived to be an ellipsoid, and the determination of its ellipticity, that is, the difference of equatorial radius and polar radius divided by the equatorial radius, became an important geodetic problem. A significant contribution to the solution of this problem was made by determinations of gravity by the pendulum.
An epoch-making work during the ellipsoidal era[Pg 309] of geodesy was Clairaut’s treatise, Théorie de la figure de la terre.[14] On the hypothesis that the earth is a spheroid of equilibrium, that is, such that a layer of water would spread all over it, and that the internal density varies so that layers of equal density are coaxial spheroids, Clairaut derived a historic theorem: If γE, γP are the values of gravity at the equator and pole, respectively, and c the centrifugal force at the equator divided by γE, then the ellipticity α = (5/2)c - (γP - γE)/γE.
Laplace showed that the surfaces of equal density might have any nearly spherical form, and Stokes showed that it is unnecessary to assume any law of density as long as the external surface is a spheroid of equilibrium.[15] It follows from Clairaut’s theorem that if the earth is an oblate spheroid, its ellipticity can be determined from relative values of gravity and the absolute value at the equator involved in c. Observations with nonreversible, invariable compound pendulums have contributed to the application of Clairaut’s theorem in its original and contemporary extended form for the determination of the figure and gravity field of the earth.
Early Types of Pendulums
The pendulum employed in observations of gravity prior to the 19th century usually consisted of a small weight suspended by a filament (figs. 4-6). The pioneer experimenters with “simple” pendulums changed the length of the suspension until the pendulum beat seconds. Picard in 1669 determined the length of the seconds pendulum at Paris with a “simple” pendulum which consisted of a copper ball an inch in diameter suspended by a fiber of pite from jaws (pite was a preparation of the leaf of a species of aloe and was not affected appreciably by moisture).
A celebrated set of experiments with a “simple” pendulum was conducted by Bouguer[16] in 1737 in the Andes, as part of the expedition to measure the Peruvian arc. The bob of the pendulum was a double truncated cone, and the length was measured from the jaw suspension to the center of oscillation of the thread and bob. Bouguer allowed for change of length of his measuring rod with temperature and also for the buoyancy of the air. He determined the time of swing by an elementary form of the method of coincidences. The thread of the pendulum was swung in front of a scale and Bouguer observed how long it took the pendulum to lose a number of vibrations on the seconds clock. For this purpose, he noted the time when the beat of the clock was heard and, simultaneously, the thread moved past the center of the scale. A historic aspect of Bouguer’s method was that he employed an “invariable” pendulum, that is, the length was maintained the same at the various stations of observation, a procedure that has been described as having been invented by Bouguer.
Since T = π√(l/g), it follows that T12/T22 = g2/g1. Thus, if the absolute value of gravity is known at one station, the value at any other station can be determined from the ratio of the squares of times of swing of an invariable pendulum at the two stations. From the above equation, if T1 is the time of swing at a station where the intensity of gravity is g, and T2 is the time at a station where the intensity is g + Δg, then (Δg)/g = (T12/T22) - 1.
Bouguer’s investigations with his invariable pendulum yielded methods for the determination of the internal structure of the earth. On the Peruvian expedition, he determined the length of the seconds pendulum at three stations, including one at Quito, at varying distances above sea level. If values of gravity at stations of different elevation are to be compared, they must be reduced to the same level, usually to sea level. Since gravity decreases with height above sea level in accordance with the law of gravitation, a free-air reduction must be applied to values of gravity determined above the level of the sea. Bouguer originated the additional reduction for the increase in gravity on a mountain or plateau caused by the attraction of the matter in a plate. From the relative values of gravity at elevated stations in Peru and at sea level, Bouguer calculated that the mean density of the earth was 4.7 times greater than that of the cordilleras.[17] For greater accuracy in the study of the internal structure of the earth, in the 19th century the Bouguer plate reduction[Pg 310] came to be supplemented by corrections for irregularities of terrain and by different types of isostatic reduction.
La Condamine, who like Bouguer was a member of the Peruvian expedition, conducted his own pendulum experiments (fig. 4). He experimented in 1735 at Santo Domingo en route to South America,[18] then at various stations in South America, and again at Paris upon his return to France. His pendulum consisted of a copper ball suspended by a thread of pite. For experimentation the length initially was about 12 feet, and the time of swing 2 seconds, but then the length was reduced to about 3 feet with time of swing 1 second. Earlier, when it was believed that gravity was constant over the earth, Picard and others had proposed that the length of the seconds pendulum be chosen as the standard. La Condamine in 1747 revived the proposal in the form that the length of the seconds pendulum at the equator be adopted as the standard of length. Subsequently, he investigated the expansion of a toise of iron from the variation in the period of his pendulum. In 1755, he observed the pendulum at Rome with Boscovich. La Condamine’s pendulum was used by other observers and finally was lost at sea on an expedition around the world. The knowledge of the pendulum acquired by the end of the 18th century was summarized in 1785 in a memoir by Boscovich.[19]
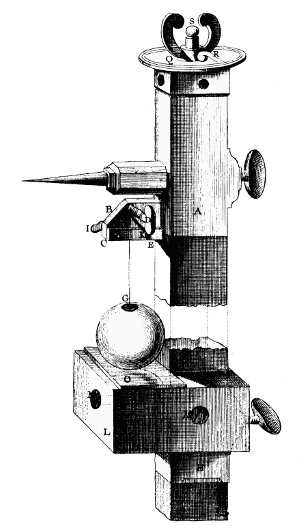
Figure 5.—An apparatus for the practice measurement of the length of the pendulum devised on the basis of a series of preliminary experiments by C. M. de la Condamine who, in the course of the French geodetic expedition to Peru in 1735, devoted a 3-month sojourn on the island of Santo Domingo to pendulum observations by Mairan’s Method. In this arrangement, shown here, a vertical rod of ironwood is used both as the scale and as the support for the apparatus, having at its top the brass pendulum support (A) and, below, a horizontal mirror (O) which serves to align the apparatus vertically through visual observation of the reflection of the pointer projecting from A. The pendulum, about 37 inches long, consists of a thread of pite (a humidity-resistant, natural fiber) and a copper ball of about 6 ounces. Its exact length is determined by adjusting the micrometer (S) so that the ball nearly touches the mirror. It will be noted that the clock pendulum would be obscured by the scale. La Condamine seems to have determined the times of coincidence by visual observation of the occasions on which “the pendulums swing parallel.” (Portion of plate 1, Mémoires publiés par la Société française de Physique, vol. 4.)

Figure 6.—The result of early pendulum experiments was often expressed in terms of the length of a pendulum which would have a period of one second and was called “the seconds pendulum.” In 1792, J. C. Borda and J. D. Cassini determined the length of the seconds pendulum at Paris with this apparatus. The pendulum consists of a platinum ball about 1-1/2 inches in diameter, suspended by a fine iron wire. The length, about 12 feet, was such that its period would be nearly twice as long as that of the pendulum of the clock (A). The interval between coincidences was determined by observing, through the telescope at the left, the times when the two pendulums emerge together from behind the screen (M). The exact length of the pendulum was measured by a platinum scale (not shown) equipped with a vernier and an auxiliary copper scale for temperature correction.
When, at the end of the 18th century, the French revolutionary government established the metric system of weights and measures, the length of the seconds pendulum at Paris was considered, but not adopted, as the unit of length. (Plate 2, Mémoires publiés par la Société française de Physique, vol. 4.)
The practice with the “simple” pendulum on the part of Picard, Bouguer, La Condamine and others in France culminated in the work of Borda and Cassini in 1792 at the observatory in Paris[20] (fig. 6). The[Pg 312] experiments were undertaken to determine whether or not the length of the seconds pendulum should be adopted as the standard of length by the new government of France. The bob consisted of a platinum ball 16-1/6 Paris lines in diameter, and 9,911 grains (slightly more than 17 ounces) in weight. The bob was held to a brass cup covering about one-fifth of its surface by the interposition of a small quantity of grease. The cup with ball was hung by a fine iron wire about 12 Paris feet long. The upper end of the wire was attached to a cylinder which was part of a wedge-shaped knife edge, on the upper surface of which was a stem on which a small adjustable weight was held by a screw thread. The knife edge rested on a steel plate. The weight on the knife-edge apparatus was adjusted so that the apparatus would vibrate with the same period as the pendulum. Thus, the mass of the suspending apparatus could be neglected in the theory of motion of the pendulum about the knife edge.
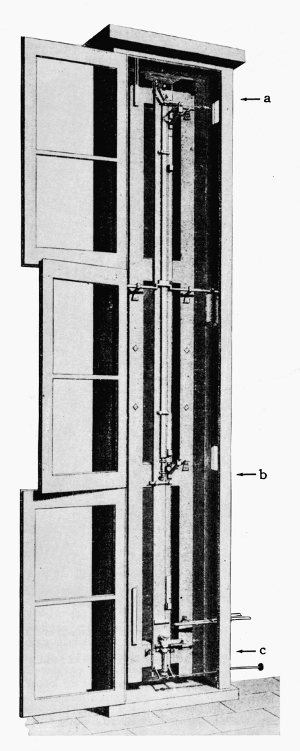
Figure 7.—Results of experiments in the determination of the length of the seconds pendulum at Königsberg by a new method were reported by F. W. Bessel in 1826 and published in 1828. With this apparatus, he obtained two sets of data from the same pendulum, by using two different points of suspension. The pendulum was about 10 feet long. The distance between the two points of suspension (a and b) was 1 toise (about six feet). A micrometric balance (c) below the bob was used to determine the increase in length due to the weight of the bob. He projected the image of the clock pendulum (not shown) onto the gravity pendulum by means of a lens, thus placing the clock some distance away and eliminating the disturbing effect of its motion. (Portion of plate 6, Mémoires publiés par la Société française de Physique, vol. 4.)
In the earlier suspension from jaws there was uncertainty as to the point about which the pendulum oscillated. Borda and Cassini hung their pendulum in front of a seconds clock and determined the time of swing by the method of coincidences. The times on the clock were observed when the clock gained or lost one complete vibration (two swings) on the pendulum. Suppose that the wire pendulum makes n swings while the clock makes 2n + 2. If the clock beats seconds exactly, the time of one complete vibration is 2 seconds, and the time of swing of the wire pendulum is T = (2n + 2)/n = 2(1 + 1/n). An error in the time caused by uncertainty in determining the coincidence of clock and wire pendulum is reduced[Pg 313] by employing a long interval of observation 2n. The whole apparatus was enclosed in a box, in order to exclude disturbances from currents of air. Corrections were made for buoyancy, for amplitude of swing and for variations in length of the wire with temperature. The final result was that the length of the seconds pendulum at the observatory in Paris was determined to be 440.5593 Paris lines, or 993.53 mm., reduced to sea level 993.85 mm. Some years later the methods of Borda were used by other French investigators, among whom was Biot who used the platinum ball of Borda suspended by a copper wire 60 cm. long.
Another historic “simple” pendulum was the one swung by Bessel (fig. 7) for the determination of gravity at Königsberg 1825-1827.[21] The pendulum consisted of a ball of brass, copper, or ivory that was suspended by a fine wire, the upper end of which was wrapped and unwrapped on a horizontal cylinder as support. The pendulum was swung first from one point and then from another, exactly a “toise de Peru”[22] higher up, the bob being at the same level in each case (fig. 7). Bessel found the period of vibration of the pendulum by the method of coincidences; and in order to avoid disturbances from the comparison clock, it was placed at some distance from the pendulum under observation.
Bessel’s experiments were significant in view of the care with which he determined the corrections. He corrected for the stiffness of the wire and for the lack of rigidity of connection between the bob and wire. The necessity for the latter correction had been pointed out by Laplace, who showed that through the circumstance that the pull of the wire is now on one side and now on the other side of the center of gravity, the bob acquires angular momentum about its center of gravity, which cannot be accounted for if the line of the wire, and therefore the force that it exerts, always passed through the center. In addition to a correction for buoyancy of the air considered by his predecessors, Bessel also took account of the inertia of the air set in motion by the pendulum.

Figure 8.—Mode of suspension of Bessel’s pendulum is shown here. The iron wire is supported by the thumbscrew and clamp at the left, but passes over a pin at the center, which is actually the upper terminal of the pendulum. Bessel found this “cylinder of unrolling” superior to the clamps and knife edges of earlier pendulums. The counterweight at the right is part of a system for supporting the scale in such a way that it is not elongated by its own weight.
With this apparatus, Bessel determined the ratio of the lengths of the two pendulums and their times of vibration. From this the length of the seconds pendulum was calculated. His method eliminated the need to take into account such sources of inaccuracy as flexure of the pendulum wire and imperfections in the shape of the bob. (Portion of plate 7, Mémoires publiés par la Société française de Physique, vol. 4.)

Figure 9.—Friedrich Wilhelm Bessel (1784-1846), German mathematician and astronomer. He became the first superintendent of the Prussian observatory established at Königsberg in 1810, and remained there during the remainder of his life. So important were his many contributions to precise measurement and calculation in astronomy that he is often considered the founder of the “modern” age in that science. This characteristic also shows in his venture into geodesy, 1826-1830, one product of which was the pendulum experiment reported in this article.
The latter effect had been discovered by Du Buat in 1786,[23] but his work was unknown to Bessel. The length of the seconds pendulum at Königsberg, reduced to sea level, was found by Bessel to be 440.8179 lines. In 1835, Bessel determined the intensity of gravity at a site in Berlin where observations later were conducted in the Imperial Office of Weights and Measures by Charles S. Peirce of the U.S. Coast Survey.
Kater’s Convertible and Invariable Pendulums

Figure 10.—Henry Kater (1777-1835), English army officer and physicist. His scientific career began during his military service in India, where he assisted in the “great trigonometrical survey.” Returned to England because of bad health, and retired in 1814, he pioneered (1818) in the development of the convertible pendulum as an alternative to the approximation of the “simple” pendulum for the measurement of the “seconds pendulum.” Kater’s convertible pendulum and the invariable pendulum introduced by him in 1819 were the basis of English pendulum work. (Photo courtesy National Portrait Gallery, London.)
Figure 11.—The attempt to approximate the simple (theoretical) pendulum in gravity experiments ended in 1817-18 when Henry Kater invented the compound convertible pendulum, from which the equivalent simple pendulum could be obtained according to the method of Huygens (see text, p. 314). Developed in connection with a project to fix the standard of English measure, Kater’s pendulum was called "compound" because it was a solid bar rather than the fine wire or string with which earlier experimenters had tried to approximate a "weightless" rod. It was called convertible because it is alternately swung from the two knife edges (a and b) at opposite ends. The weights (f and g) are adjusted so that the period of the pendulum is the same from either knife edge. The distance between the two knife edges is then equal to the length of the equivalent simple pendulum.
The systematic survey of the gravity field of the earth was given a great impetus by the contributions of Capt. Henry Kater, F.R.S. In 1817, he designed, constructed, and applied a convertible compound pendulum for the absolute determination of gravity at the house of Henry Browne, F.R.S., in Portland Place, London.[24] Kater’s convertible pendulum (fig. 11) consisted of a brass rod to which were attached a flat circular bob of brass and two adjustable weights, the smaller of which was adjusted by a screw. The convertibility of the pendulum was constituted by the provision of two knife edges turned inwards on opposite sides of the center of gravity. The pendulum was swung on each knife edge, and the adjustable weights were moved until the times of swing were the same about each knife edge. When the times were judged to be the same, the distance between the knife edges was inferred to be the length of the equivalent simple pendulum, in accordance with Huygens’ theorem on conjugate points of a compound pendulum. Kater determined the time of swing by the method of coincidences (fig. 12). He corrected for the buoyancy of the air. The final value of the length of the seconds pendulum at Browne’s house in London, reduced to sea level, was determined to be 39.13929 inches.
The convertible compound pendulum had been conceived prior to its realization by Kater. In 1792, on the occasion of the proposal in Paris to establish the standard of length as the length of the seconds pendulum, Baron de Prony had proposed the employment of a compound pendulum with three axes of oscillation.[25] In 1800, he proposed the convertible compound pendulum with knife edges about which the pendulum could complete swings in equal times. De Prony’s proposals were not accepted and his papers remained unpublished until 1889, at which time they were discovered by Defforges. The French decision was to experiment with the ball pendulum, and the determination of the length of the seconds[Pg 315] pendulum was carried out by Borda and Cassini by methods previously described. Bohnenberger in his Astronomie (1811),[26] made the proposal to employ a convertible pendulum for the absolute determination of gravity; thus, he has received credit for priority in publication. Capt. Kater independently conceived of the convertible pendulum and was the first to design, construct, and swing one.
After his observations with the convertible pendulum, Capt. Kater designed an invariable compound pendulum with a single knife edge but otherwise similar in external form to the convertible pendulum[27] (fig. 13). Thirteen of these Kater invariable pendulums have been reported as constructed and swung at stations throughout the world.[28] Kater himself swung an invariable pendulum at a station in London and at various other stations in the British Isles. Capt. Edward Sabine, between 1820 and 1825, made voyages and swung Kater invariable pendulums at stations from the West Indies to Greenland and Spitzbergen.[29] In 1820, Kater swung a Kater invariable pendulum at London and then sent it to Goldingham, who swung it in 1821 at Madras, India.[30] Also in 1820, Kater supplied an invariable pendulum to Hall, who swung it at London and then made observations near the equator and in the Southern Hemisphere, and at London again in 1823.[31] The same pendulum, after its knives were reground, was delivered to Adm. Lütke of Russia, who observed gravity with it on a trip around the world between 1826 and 1829.[32]

Figure 12.—The Kater convertible pendulum in use is placed before a clock, whose pendulum bob is directly behind the extended “tail” of the Kater pendulum. A white spot is painted on the center of the bob of the clock pendulum. The observing telescope, left, has a diaphragm with a vertical slit of such width that its view is just filled by the tail of the Kater pendulum when it is at rest. When the two pendulums are swinging, the white spot on the clock pendulum can be seen on each swing except that in which the two pendulums are in coincidence; thus, the coincidences are determined. (Portion of plate 5, Mémoires publiés par la Société française de Physique, vol. 4.)[Pg 317]

Figure 13.—This drawing accompanied John Goldingham’s report on the work done in India with Kater’s invariable pendulum. The value of gravity obtained, directly or indirectly, in terms of the simple pendulum, is called “absolute.” Once absolute values of gravity were established at a number of stations, it became possible to use the much simpler “relative” method for the measurement of gravity at new stations. Because it has only one knife edge, and does not involve the adjustments of the convertible pendulum, this one is called “invariable.” In use, it is first swung at a station where the absolute value of gravity has been established, and this period is then compared with its period at one or more new stations. Kater developed an invariable pendulum in 1819, which was used in England and in Madras, India, in 1821.
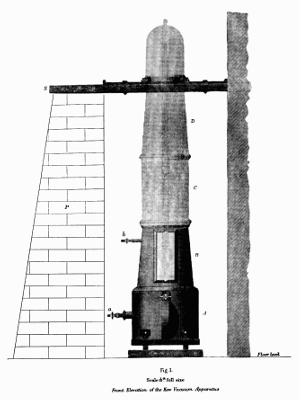
Figure 14.—Vacuum chamber for use with the Kater pendulum. Of a number of extraneous effects which tend to disturb the accuracy of pendulum observations the most important is air resistance. Experiments reported by the Greenwich (England) observatory in 1829 led to the development of a vacuum chamber within which the pendulum was swung.
While the British were engaged in swinging the Kater invariable pendulums to determine relative values of the length of the seconds pendulum, or of gravity, the French also sent out expeditions. Capt. de Freycinet made initial observations at Paris with three invariable brass pendulums and one wooden one, and then carried out observations at Rio de Janeiro, Cape of Good Hope, Île de France, Rawak (near New Guinea), Guam, Maui, and various other places.[33] A similar expedition was conducted in 1822-1825 by Captain Duperry.[34]
During the years from 1827 to 1840, various types of pendulum were constructed and swung by Francis Baily, a member of the Royal Astronomical Society, who reported in 1832 on experiments in which no less than 41 different pendulums were swung in vacuo, and their characteristics determined.[35] In 1836, Baily undertook to advise the American Lt. Charles Wilkes, who was to head the United States Exploring[Pg 318] Expedition of 1838-1842, on the procurement of pendulums for this voyage. Wilkes ordered from the London instrument maker, Thomas Jones, two unusual pendulums, which Wilkes described as “those considered the best form by Mr. Baily for traveling pendulums,” and which Baily, himself, described as “precisely the same as the two invariable pendulums belonging to this [Royal Astronomical] Society,” except for the location of the knife edges.

Figure 15.—One of Francis Baily’s pendulums (62-1/2 inches long), shown on the left, is now in the possession of the Science Museum, London, and, right, two views of a similar pendulum (37-5/8 inches long) made in the late 19th century by Edward Kübel, Washington, D.C., which is no. 316,876 in the collection of the U.S. National Museum. Among a large number of pendulums tried by Baily in London (1827-1840), was one which resembles the reversible pendulum superficially, but which is actually an invariable pendulum having knife edges at both ends. The purpose was apparently economy, since it is equivalent to two separate invariable pendulums. This is the type of pendulum used on the U.S. Exploring Expedition of 1838-1842. It is not known what use was made of the Kübel pendulum.
The unusual feature of these pendulums was in their symmetry of mass as well as of form. They were made of bars, of iron in one case, and of brass in the other, and each had two knife edges at opposite ends equidistant from the center. Thus, although they resembled reversible pendulums, their symmetry of mass prevented their use as such, and they were rather equivalent to four separate invariable pendulums.[36]
Wilkes was taught the use of the pendulum by Baily, and conducted experiments at Baily’s house, where the latter had carried out the work reported on in 1832. The subsequent experiments made on the U.S. Exploring Expedition were under the charge of Wilkes, himself, who made observations on 11 separate occasions, beginning with that in London (1836) and followed by others in New York, Washington, D.C., Rio de Janeiro, Sydney, Honolulu, “Pendulum Peak” (Mauna Loa), Mount Kanoha, Nesqually (Oregon Territory), and, finally, two more times in Washington, D.C. (1841 and 1845).
Wilkes’ results were communicated to Baily, who appears to have found the work defective because of insufficient attention to the maintenance of temperature constancy and to certain alterations made to the pendulums.[37] The results were also to have been included in the publications of the Expedition, but were part of the unpublished 24th volume. Fortunately they still exist, in what appears to be a printer’s proof.[38]
The Kater invariable pendulums were used to investigate the internal constitution of the earth. Airy sought to determine the density of the earth by observing the times of swing of pendulums at the top and bottom of a mine. The first experiments were made in 1826 at the Dolcoath copper mine in Cornwall, and failed when the pendulum fell to the bottom.[Pg 319] In 1854, the experiments were again undertaken in the Harton coalpit, near Sunderland.[39] Gravity at the surface was greater than below, because of the attraction of a shell equal to the depth of the pit. From the density of the shell as determined from specimens of rock, Airy found the density of the earth to be 6-1/2 times greater than that of water. T. C. Mendenhall, in 1880, used a Kater convertible pendulum in an invariable manner to compare values of gravity on Fujiyama and at Tokyo, Japan.[40] He used a “simple” pendulum of the Borda type to determine the absolute value of gravity at Tokyo. From the values of gravity on the mountain and at Tokyo, and an estimate of the volume of the mountain, he estimated the mean density of the earth as 5.77 times greater than that of water.
In 1879, Maj. J. Herschel, R.E., stated:
The years from 1840 to 1865 are a complete blank, if we except Airy’s relative density experiments in 1854. This pause was broken simultaneously in three different ways. Two pendulums of the Kater pattern were sent to India; two after Bessel’s design were set to work in Russia; and at Geneva, Plantamour’s zealous experiments with a pendulum of the same kind mark the commencement of an era of renewed activity on the European continent.[41]
With the statement that Kater invariable pendulums nos. 4 and 6 (1821) were used in India between 1865 and 1873, we now consider the other events mentioned by Herschel.
Repsold-Bessel Reversible Pendulum
As we have noted, Bessel made determinations of gravity with a ball (“simple”) pendulum in the period 1825-1827 and in 1835 at Königsberg and Berlin, respectively. In the memoir on his observations at Königsberg, he set forth the theory of the symmetrical compound pendulum with interchangeable knife edges.[42] Bessel demonstrated theoretically that if the pendulum were symmetrical with respect to its geometrical center, if the times of swing about each axis were the same, the effects of buoyancy and of air set in motion would be eliminated. Laplace had already shown that the knife edge must be regarded as a cylinder and not as a mere line of support. Bessel then showed that if the knife edges were equal cylinders, their effects were eliminated by inverting the pendulum; and if the knife edges were not equal cylinders, the difference in their effects was canceled by interchanging the knives and again determining the times of swing in the so-called erect and inverted positions. Bessel further showed that it is unnecessary to make the times of swing exactly equal for the two knife edges.
The simplified discussion for infinitely small oscillations in a vacuum is as follows: If T1 and T2 are the times of swing about the knife edges, and if h1 and h2 are distances of the knife edges from the center of gravity, and if k is the radius of gyration about an axis through the center of gravity, then from the equation of motion of a rigid body oscillating about a fixed axis under gravity T12 = π2(k2 + h12)/gh1, T22 = π2(k2 + h22)/gh2. Then (h1T12 - h2T22)/(h1 - h2) = (π2/g)(h1 + h2) = τ2.
τ is then the time of swing of a simple pendulum of length h1 + h2. If the difference T1 - T2 is sufficiently small, τ = (h1T1 - h2T2)/(h1 - h2). Prior to its publication by Bessel in 1828, the formula for the time of swing of a simple pendulum of length h1 + h2 in terms of T1, T2 had been given by C. F. Gauss in a letter to H. C. Schumacher dated November 28, 1824.[43]
The symmetrical compound pendulum with interchangeable knives, for which Bessel gave a posthumously published design and specifications,[44] has been called a reversible pendulum; it may thereby be distinguished from Kater’s unsymmetrical convertible pendulum. In 1861, the Swiss Geodetic Commission was formed, and in one of its first sessions in 1862 it was decided to add determinations of gravity to the operations connected with the measurement—at different points in Switzerland—of the arc of the meridian traversing central Europe.[45] It was decided further to employ a reversible pendulum of Bessel’s design and to have it constructed by the firm of A. Repsold and Sons, Hamburg. It was also decided to make the first observations with the pendulum in Geneva; accordingly, the Repsold-Bessel pendulum (fig. 16) was sent to Prof. E. Plantamour, director of the observatory at Geneva, in the autumn of 1864.[46]
The Swiss reversible pendulum was about 560 mm. in length (distance between the knife edges) and the time of swing was approximately 3/4-second. At the extremities of the stem of the pendulum were movable cylindrical disks, one of which was solid and heavy, the other hollow and light. It was intended by the mechanicians that equality of times of oscillation about the knife edges would be achieved by adjusting the position of a movable disk. The pendulum was hung by a knife edge on a plate supported by a tripod and having an attachment from which a measuring rod could be suspended so that the distance between the knife edges could be measured by a comparator. Plantamour found it impracticable to adjust a disk until the times of swing about each knife edge were equal. His colleague, Charles Cellérier,[47] [Pg 321]then showed that if (T1 - T2)/T1 is sufficiently small so that one can neglect its square, one can determine the length of the seconds pendulum from the times of swing about the knife edges by a theory which uses the distances of the center of gravity from the respective knife edges. Thus, a role for the position of the center of gravity in the theory of the reversible pendulum, which had been set forth earlier by Bessel, was discovered independently by Cellérier for the Swiss observers of pendulums.
In 1866, Plantamour published an extensive memoir “Expériences faites à Genève avec le pendule à réversion.” Another memoir, published in 1872, presented further results of determinations of gravity in Switzerland. Plantamour was the first scientist in western Europe to use a Repsold-Bessel reversible pendulum and to work out methods for its employment.
The Russian Imperial Academy of Sciences acquired two Repsold-Bessel pendulums, and observations with them were begun in 1864 by Prof. Sawitsch, University of St. Petersburg, and others.[48] In 1869, the Russian pendulums were loaned to the India Survey in order to enable members of the Survey to supplement observations with the Kater invariable pendulums nos. 4 and 6 (1821). During the transport of the Russian apparatus to India, the knives became rusted and the apparatus had to be reconditioned. Capt. Heaviside of the India Survey observed with both pendulums at Kew Observatory, near London, in the spring of 1874, after which the Russian pendulums were sent to Pulkowa (Russia) and were used for observations there and in the Caucasus.
The introduction of the Repsold-Bessel reversible pendulum for the determination of gravity was accompanied by the creation of the first international scientific association, one for geodesy. In 1861, Lt. Gen. J. J. Baeyer, director of the Prussian Geodetic Survey, sent a memorandum to the Prussian minister of war in which he proposed that the independent geodetic surveys of the states of central Europe be coordinated by the creation of an international organization.[49] In 1862, invitations were sent to the various German states and to other states of central Europe. The first General Conference of the association, initially called Die Mittel-Europäische Gradmessung, also L’Association Géodésique Internationale, was[Pg 322] held from the 15th to the 22d of October 1864 in Berlin.[50] The Conference decided upon questions of organization: a general conference was to be held ordinarily every three years; a permanent commission initially consisting of seven members was to be the scientific organ of the association and to meet annually; a central bureau was to be established for the reception, publication, and distribution of reports from the member states.
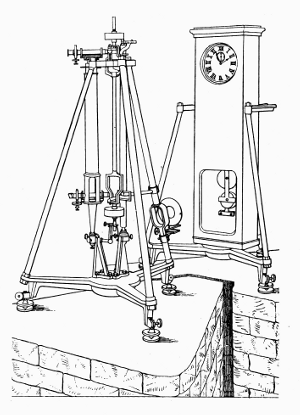
Figure 16.—From a Design Left by Bessel, this portable apparatus was developed in 1862 by the firm of Repsold in Hamburg, whose founder had assisted Bessel in the construction of his pendulum apparatus of 1826. The pendulum is convertible, but differs from Kater’s in being geometrically symmetrical and, for this reason, Repsold’s is usually called “reversible.” Just to the right of the pendulum is a standard scale. To the left is a “vertical comparator” designed by Repsold to measure the distance between the knife edges of the pendulum. To make this measurement, two micrometer microscopes which project horizontally through the comparator are alternately focused on the knife edges and on the standard scale.
Under the topic “Astronomical Questions,” the General Conference of 1864 resolved that there should be determinations of the intensity of gravity at the greatest possible number of points of the geodetic network, and recommended the reversible pendulum as the instrument of observation.[51] At the second General Conference, in Berlin in 1867, on the basis of favorable reports by Dr. Hirsch, director of the observatory at Neuchâtel, of Swiss practice with the Repsold-Bessel reversible pendulum, this instrument was specifically recommended for determinations of gravity.[52] The title of the association was changed to Die Europäische Gradmessung; in 1886, it became Die Internationale Erdmessung, under which title it continued until World War I.
On April 1, 1866, the Central Bureau of Die Europäische Gradmessung was opened in Berlin under the presidency of Baeyer, and in 1868 there was founded at Berlin, also under his presidency, the Royal Prussian Geodetic Institute, which obtained regular budgetary status on January 1, 1870. A reversible pendulum for the Institute was ordered from A. Repsold and Sons, and it was delivered in the spring of 1869. The Prussian instrument was symmetrical geometrically, as specified by Bessel, but different in form from the Swiss and Russian pendulums. The distance between the knife edges was 1 meter, and the time of swing approximately 1 second. The Prussian Repsold-Bessel pendulum was swung at Leipzig and other stations in central Europe during the years 1869-1870 by Dr. Albrecht under the direction of Dr. Bruhns, director of the observatory at Leipzig and chief of the astronomical section of the Geodetic Institute. The results of these first observations appeared in a publication of the Royal Prussian Geodetic Institute in 1871.[53]
Results of observations with the Russian Repsold-Bessel pendulums were published by the Imperial Academy of Sciences. In 1872, Prof. Sawitsch reported the work for western Europeans in “Les variations de la pesanteur dans les provinces occidentales de l’Empire russe.”[48] In November 1873, the Austrian Geodetic Commission received a Repsold-Bessel reversible pendulum and on September 24, 1874, Prof. Theodor von Oppolzer reported on observations at Vienna and other stations to the Fourth General Conference of Die Europäische Gradmessung in Dresden.[54] At the fourth session of the Conference, on September 28, 1874, a Special Commission, consisting of Baeyer, as chairman, and Bruhns, Hirsch, Von Oppolzer, Peters, and Albrecht, was appointed to consider (under Topic 3 of the program): “Observations for the determination of the intensity of gravity,” the question, “Which Pendulum-apparatuses are preferable for the determination of many points?”
After the adoption of the Repsold-Bessel reversible pendulum for gravity determinations in Europe, work in the field was begun by the U.S. Coast Survey under the superintendency of Prof. Benjamin Peirce. There is mention in reports of observations with pendulums prior to Peirce’s direction to his son Charles on November 30, 1872, “to take charge of the Pendulum Experiments of the Coast Survey and to direct and inspect all parties engaged in such experiments and as often as circumstances will permit, to take the field with a party....”[55] Systematic and important gravity work by the Survey was begun by Charles Sanders[Pg 323] Peirce. Upon receiving notice of his appointment, the latter promptly ordered from the Repsolds a pendulum similar to the Prussian instrument. Since the firm of mechanicians was engaged in making instruments for observations of the transit of Venus in 1874, the pendulum for the Coast Survey could not be constructed immediately. Meanwhile, during the years 1873-1874, Charles Peirce conducted a party which made observations of gravity in the Hoosac Tunnel near North Adams, and at Northampton and Cambridge, Massachusetts. The pendulums used were nonreversible, invariable pendulums with conical bobs. Among them was a silver pendulum, but similar pendulums of brass were used also.[56]

Figure 17.—Repsold-Bessel reversible pendulum apparatus as made in 1875, and used in the gravity work of the U.S. Coast and Geodetic Survey. Continental geodesists continued to favor the general use of convertible pendulums and absolute determinations of gravity, while their English colleagues had turned to invariable pendulums and relative determinations, except for base stations. Perhaps the first important American contribution to gravity work was C. S. Peirce’s demonstration of the error inherent in the Repsold apparatus through flexure of the stand.

Figure 18.—Charles Sanders Peirce (1839-1914), son of Benjamin Peirce, Perkins Professor of Astronomy and Mathematics at Harvard College. C. S. Peirce graduated from Harvard in 1859. From 1873 to 1891, as an assistant at the U.S. Coast and Geodetic Survey, he accomplished the important gravimetric work described in this article. Peirce was also interested in many other fields, but above all in the logic, philosophy, and history of science, in which he wrote extensively. His greatest fame is in philosophy, where he is regarded as the founder of pragmatism.
[Pg 324]In 1874, Charles Peirce expressed the desire to be sent to Europe for at least a year, beginning about March 1, 1875, “to learn the use of the new convertible pendulum and to compare it with those of the European measure of a Degree and the Swiss and to compare” his “invariable pendulums in the manner which has been used by swinging them in London and Paris.”[57]
Charles S. Peirce, assistant, U.S. Coast Survey, sailed for Europe on April 3, 1875, on his mission to obtain the Repsold-Bessel reversible pendulum ordered for the Survey and to learn the methods of using it for the determination of gravity. In England, he conferred with Maxwell, Stokes, and Airy concerning the theory and practice of research with pendulums. In May, he continued on to Hamburg and obtained delivery from the Repsolds of the pendulum for the Coast Survey (fig. 17). Peirce then went to Berlin and conferred with Gen. Baeyer, who expressed doubts of the stability of the Repsold stand for the pendulum. Peirce next went to Geneva, where, under arrangements with Prof. Plantamour, he swung the newly acquired pendulum at the observatory.[58]
In view of Baeyer’s expressed doubts of the rigidity of the Repsold stand, Peirce performed experiments to measure the flexure of the stand caused by the oscillations of the pendulum. His method was to set up a micrometer in front of the pendulum stand and, with a microscope, to measure the displacement caused by a weight passing over a pulley, the friction of which had been determined. Peirce calculated the correction to be applied to the length of the seconds pendulum—on account of the swaying of the stand during the swings of the pendulum—to amount to over 0.2 mm. Although Peirce’s measurements of flexure in Geneva were not as precise as his later measurements, he believed that failure to correct for flexure of the stand in determinations previously made with Repsold pendulums was responsible for appreciable errors in reported values of the length of the seconds pendulum.
The Permanent Commission of Die Europäische Gradmessung met in Paris, September 20-29, 1875. In conjunction with this meeting, there was held on September 21 a meeting of the Special Commission on the Pendulum. The basis of the discussion by the Special Commission was provided by reports which had been submitted in response to a circular sent out by the Central Bureau to the members on February 26, 1874.[59]
Gen. Baeyer stated that the distance of 1 meter between the knife edges of the Prussian Repsold-Bessel pendulum made it unwieldy and unsuited for transport. He declared that the instability of the stand also was a source of error. Accordingly, Gen. Baeyer expressed the opinion that absolute determinations of gravity should be made at a control station by a reversible pendulum hung on a permanent, and therefore stable stand, and he said that relative values of gravity with respect to the control station should be obtained in the field by means of a Bouguer invariable pendulum. Dr. Bruhns and Dr. Peters agreed with Gen. Baeyer; however, the Swiss investigators, Prof. Plantamour and Dr. Hirsch reported in defense of the reversible pendulum as a field instrument, as did Prof. von Oppolzer of Vienna. The circumstance that an invariable pendulum is subject to changes in length was offered as an argument in favor of the reversible pendulum as a field instrument.
Peirce was present during these discussions by the members of the Special Commission, and he reported that his experiments at Geneva demonstrated that the oscillations of the pendulum called forth a flexure of the support which hitherto had been neglected. The observers who used the Swiss and Austrian Repsold pendulums contended, in opposition to Peirce, that the Repsold stand was stable.
The outcome of these discussions was that the Special Commission reported to the Permanent Commission that the Repsold-Bessel reversible pendulum, except for some small changes, satisfied all requirements for the determination of gravity. The Special Commission proposed that the Repsold pendulums of the several states be swung at the Prussian Eichungsamt in Berlin where, as Peirce pointed out, Bessel had made his determination of the intensity of gravity with a ball pendulum in 1835. Peirce was encouraged to swing the Coast Survey reversible pendulum at the stations in France, England, and Germany where[Pg 325] Borda and Cassini, Kater, and Bessel, respectively, had made historic determinations. The Permanent Commission, in whose sessions Peirce also participated, by resolutions adopted the report of the Special Commission on the Pendulum.[60]
During the months of January and February 1876, Peirce conducted observations in the Grande Salle du Meridien at the observatory in Paris where Borda, Biot, and Capt. Edward Sabine had swung pendulums early in the 19th century. He conducted observations in Berlin from April to June 1876 and, by experiment, determined the correction for flexure to be applied to the value of gravity previously obtained with the Prussian instrument. Subsequent observations were made at Kew. After his return to the United States on August 26, 1876, Peirce conducted experiments at the Stevens Institute in Hoboken, New Jersey, where he made careful measurements of the flexure of the stand by statical and dynamical methods. In Geneva, he had secured the construction of a vacuum chamber in which the pendulum could be swung on a support which he called the Geneva support. At the Stevens Institute, Peirce swung the Repsold-Bessel pendulum on the Geneva support and determined the effect of different pressures and temperatures on the period of oscillation of the pendulum. These experiments continued into 1878.[61]
Meanwhile, the Permanent Commission met October 5-10, 1876, in Brussels and continued the discussion of the pendulum.[62] Gen. Baeyer reported on Peirce’s experiments in Berlin to determine the flexure of the stand. The difference of 0.18 mm. in the lengths of the seconds pendulum as determined by Bessel and as determined by the Repsold instrument agreed with Peirce’s estimate of error caused by neglect of flexure of the Repsold stand. Dr. Hirsch, speaking for the Swiss survey, and Prof. von Oppolzer, speaking for the Austrian survey, contended, however, that their stands possessed sufficient stability and that the results found by Peirce applied only to the stands and bases investigated by him. The Permanent Commission proposed further study of the pendulum.
The Fifth General Conference of Die Europäische Gradmessung was held from September 27 to October 2, 1877, in Stuttgart.[63] Peirce had instructions from Supt. Patterson of the U.S. Coast Survey to attend this conference, and on arrival presented a letter of introduction from Patterson requesting that he, Peirce, be permitted to participate in the sessions. Upon invitation from Prof. Plantamour, as approved by Gen. Ibañez, president of the Permanent Commission, Peirce had sent on July 13, 1877, from New York, the manuscript of a memoir titled “De l’Influence de la flexibilité du trépied sur l’oscillation du pendule à réversion.” This memoir and others by Cellérier and Plantamour confirming Peirce’s work were published as appendices to the proceedings of the conference. As appendices to Peirce’s contribution were published also two notes by Prof. von Oppolzer. At the second session on September 29, 1877, when Plantamour reported that the work of Hirsch and himself had confirmed experimentally the independent theoretical work of Cellérier and the theoretical and experimental work of Peirce on flexure, Peirce described his Hoboken experiments.
During the discussions at Stuttgart on the flexure of the Repsold stand, Hervé Faye, president of the Bureau of Longitudes, Paris, suggested that the swaying of the stand during oscillations of the pendulum could be overcome by the suspension from one support of two similar pendulums which oscillated with equal amplitudes and in opposite phases. This proposal was criticized by Dr. Hirsch, who declared that exact observation of passages of a “double pendulum” would be difficult and that two pendulums swinging so close together would interfere with each other. The proposal of the double pendulum came up again at the meeting of the Permanent Commission at Geneva in 1879.[64] On February 17, 1879, Peirce had completed a paper “On a Method of Swinging Pendulums for the Determination of Gravity, Proposed by M.[Pg 326] Faye.” In this paper, Peirce presented the results of an analytical mechanical investigation of Faye’s proposal. Peirce set up the differential equations, found the solutions, interpreted them physically, and arrived at the conclusion “that the suggestion of M. Faye ... is as sound as it is brilliant and offers some peculiar advantages over the existing method of swinging pendulums.”
In a report to Supt. Patterson, dated July 1879, Peirce stated: “I think it is important before making a new pendulum apparatus to experiment with Faye’s proposed method.”[65] He wrote further: “The method proves to be perfectly sound in theory, and as it would greatly facilitate the work it is probably destined eventually to prevail. We must unfortunately leave to other surveys the merit of practically testing and introducing the new method, as our appropriations are insufficient for us to maintain the leading position in this matter, which we otherwise might take.” Copies of the published version of Peirce’s remarks were sent to Europe. At a meeting of the Academy of Sciences in Paris on September 1, 1879, Faye presented a report on Peirce’s findings.[66] The Permanent Commission met September 16-20, 1879, in Geneva. At the third session on September 19, by action of Gen. Baeyer, copies of Peirce’s paper on Faye’s proposed method of swinging pendulums were distributed. Dr. Hirsch again commented adversely on the proposal, but moved that the question be investigated and reported on at the coming General Conference. The Permanent Commission accepted the proposal of Dr. Hirsch, and Prof. Plantamour was named to report on the matter at the General Conference. At Plantamour’s request, Charles Cellérier was appointed to join him, since the problem essentially was a theoretical one.
The Sixth General Conference of Die Europäische Gradmessung met September 13-16, 1880, in Munich.[67] Topic III, part 7 of the program was entitled “On Determinations of Gravity through pendulum observations. Which construction of a pendulum apparatus corresponds completely to all requirements of science? Special report on the pendulum.”

Figure 19.—Three pendulums used in early work at the U.S. Coast and Geodetic Survey. Shown on the left is the Peirce invariable; center, the Peirce reversible; and, right, the Repsold reversible. Peirce designed the cylindrical pendulum in 1881-1882 to study the effect of air resistance according to the theory of G. G. Stokes on the motion of a pendulum in a viscous field. Three examples of the Peirce pendulums are in the U.S. National Museum.
The conference received a memoir by Cellérier[68] on the theory of the double pendulum and a report by Plantamour and Cellérier.[69] Cellérier’s mathematical analysis began with the equations of Peirce and used the latter’s notation as far as possible. His general discussion included the results of Peirce, but he stated that the difficulties to be overcome did not justify the employment of the “double pendulum.” He presented an alternative method of correcting for flexure based upon a theory by which the flexure caused by the oscillation of a given reversible pendulum could be determined from the behavior of an auxiliary pendulum of the same length but of different weight. This method of correcting for flexure was recommended to the General Conference by Plantamour and Cellérier in their joint report. At the fourth session of the conference on September 16, 1880, the problem of the pendulum was discussed and, in consequence, a commission consisting of Faye, Helmholtz, Plantamour (replaced in 1882 by Hirsch), and Von Oppolzer was appointed to study apparatus suitable for relative determinations of gravity.
The Permanent Commission met September 11-15, 1882, at The Hague,[70] and at its last session appointed Prof. von Oppolzer to report to the Seventh General Conference on different forms of apparatus for the determination of gravity. The Seventh Conference met October 15-24, 1883, in Rome,[71] and, at its eighth session, on October 22, received a comprehensive, critical review from Prof. von Oppolzer entitled “Über die Bestimmung der Schwere mit Hilfe verschiedener Apparate.”[72] Von Oppolzer especially expounded the advantages of the Bessel reversible pendulum, which compensated for air effects by symmetry of form if the times of swing for both positions were maintained between the same amplitudes, and compensated for irregular knife edges by making them interchangeable. Prof. von Oppolzer reviewed the problem of flexure of the Repsold stand and stated that a solution in the right direction was[Pg 327] the proposal—made by Faye and theoretically pursued by Peirce—to swing two pendulums from the same stand with equal amplitudes and in opposite phases, but that the proposal was not practicable. He concluded that for absolute determinations of gravity, the Bessel reversible pendulum was highly appropriate if one swung two exemplars of different weight from the same stand for the elimination of flexure. Prof. von Oppolzer’s important report recognized that absolute determinations were less accurate than relative ones, and should be conducted only at special places.
The discussions initiated by Peirce’s demonstration of the flexure of the Repsold stand resulted, finally, in the abandonment of the plan to make absolute determinations of gravity at all stations with the reversible pendulum.
Peirce and Defforges Invariable, Reversible Pendulums
The Repsold-Bessel reversible pendulum was designed and initially used to make absolute determinations of gravity not only at initial stations such as Kew, the observatory in Paris, and the Smithsonian Institution in Washington, D.C., but also at stations in the field. An invariable pendulum with a single knife edge, however, is adequate for relative determinations. As we have seen, such invariable pendulums had been used by Bouguer and Kater, and after the experiences with the Repsold apparatus had been recommended again by Baeyer for relative determinations. But an invariable pendulum is subject to uncontrollable changes of length. Peirce proposed to detect such changes in an invariable pendulum in the field by combining the invariable and reversible principles. He explained his proposal to Faye in a letter dated July 23, 1880, and he presented it on September 16, 1880, at the fourth session of the sixth General Conference of Die Europäische Gradmessung, in Munich.[73]
As recorded in the Proceedings of the Conference, Peirce wrote:
But I obviate it in making my pendulum both invariable and reversible. Every alteration of the pendulum will be revealed immediately by the change in the difference of the two periods of oscillation in the two positions. Once discovered, it will be taken account of by means of new measures of the distance between the two supports.
Peirce added that it seemed to him that if the reversible pendulum perhaps is not the best instrument to determine absolute gravity, it is, on condition that it be truly invariable, the best to determine relative gravity. Peirce further stated that he would wish that the pendulum be formed of a tube of drawn brass with heavy plugs of brass equally drawn. The cylinder would be terminated by two hemispheres; the knives would be attached to tongues fixed near the ends of the cylinder.
During the years 1881 and 1882, four invariable, reversible pendulums were made after the design of Peirce at the office of the U.S. Coast and Geodetic Survey in Washington, D.C. The report of the superintendent for the year 1880-1881 states:
A new pattern of the reversible pendulum has been invented, having its surface as nearly as convenient in the form of an elongated ellipsoid. Three of these instruments have been constructed, two having a distance of one meter between the knife edges and the third a distance of one yard. It is proposed to swing one of the meter pendulums at a temperature near 32° F. at the same time that the yard is swung at 60° F., in order to determine anew the relation between the yard and the meter.[74]
The report for 1881-1882 mentions four of these Peirce pendulums.
A description of the Peirce invariable, reversible pendulums was given by Assistant E. D. Preston in “Determinations of Gravity and the Magnetic Elements in Connection with the United States Scientific Expedition to the West Coast of Africa, 1889-90.”[75] The invariable, reversible pendulum, Peirce no. 4, now preserved in the Smithsonian Institution’s Museum of History and Technology (fig. 34), may be taken as typical of the meter pendulums: In the same memoir, Preston gives the diameter of the tube as 63.7 mm., thickness of tube 1.5 mm., weight 10.680 kilograms, and distance between the knives 1.000 meter.
The combination of invariability and reversibility in the Peirce pendulums was an innovation for relative determinations. Indeed, the combination was criticized by Maj. J. Herschel, R.E., of the Indian Survey, at a conference on gravity held in Washington in May 1882 on the occasion of his visit to the United States for the purpose of connecting English and American stations by relative determinations with three Kater invariable pendulums. These three pendulums have been designated as nos. 4, 6 (1821), and 11.[76]
Figure 20.—Support for the Peirce pendulum, 1889. Much of the work of C. S. Peirce was concerned with the determination of the error introduced into observations made with the portable apparatus by the vibration of the stand with the pendulum. He showed that the popular Bessel-Repsold apparatus was subject to such an error. His own pendulums were swung from a simple but rugged wooden frame to which a hardened steel bearing was fixed.
Another novel characteristic of the Peirce pendulums was the mainly cylindrical form. Prof. George Gabriel Stokes, in a paper “On the Effect of the[Pg 329] Internal Friction of Fluids on the Motion of Pendulums”[77] that was read to the Cambridge Philosophical Society on December 9, 1850, had solved the hydrodynamical equations to obtain the resistance to the motions of a sphere and a cylinder in a viscous fluid. Peirce had studied the effect of viscous resistance on the motion of his Repsold-Bessel pendulum, which was symmetrical in form but not cylindrical. The mainly cylindrical form of his pendulums (fig. 19) permitted Peirce to predict from Stokes’ theory the effect of viscosity and to compare the results with experiment. His report of November 20, 1889, in which he presented the comparison of experimental results with the theory of Stokes, was not published.[78]
Peirce used his pendulums in 1883 to establish a station at the Smithsonian Institution that was to serve as the base station for the Coast and Geodetic Survey for some years. Pendulum Peirce no. 1 was swung at Washington in 1881 and was then taken by the party of Lieutenant Greely, U.S.A., on an expedition to Lady Franklin Bay where it was swung in 1882 at Fort Conger, Grinnell Land, Canada. Peirce nos. 2 and 3 were swung by Peirce in 1882 at Washington, D.C.; Hoboken, New Jersey; Montreal, Canada; and Albany, New York. Assistant Preston took Peirce no. 3 on a U.S. eclipse expedition to the Caroline Islands in 1883. Peirce in 1885 swung pendulums nos. 2 and 3 at Ann Arbor, Michigan; Madison, Wisconsin; and Ithaca, New York. Assistant Preston in 1887 swung Peirce nos. 3 and 4 at stations in the Hawaiian Islands, and in 1890 he swung Peirce nos. 3 and 4 at stations on the west coast of Africa.[79]
The new pattern of pendulum designed by Peirce was also adopted in France, after some years of experience with a Repsold-Bessel pendulum. Peirce in 1875 had swung his Repsold-Bessel pendulum at the observatory in Paris, where Borda and Cassini, and Biot, had made historic observations and where Sabine also had determined gravity by comparison with Kater’s value at London. During the spring of 1880, Peirce made studies of the supports for the pendulums of these earlier determinations and calculated corrections to those results for hydrodynamic effects, viscosity, and flexure. On June 14, 1880, Peirce addressed the Academy of Sciences, Paris, on the value of gravity at Paris, and compared his results with the corrected results of Borda and Biot and with the transferred value of Kater.[80]
In the same year the French Geographic Service of the Army acquired a Repsold-Bessel reversible pendulum of the smaller type, and Defforges conducted experiments with it.[81] He introduced the method of measuring flexure from the movement of interference fringes during motion of the pendulum. He found an appreciable difference between dynamical and statical coefficients of flexure and concluded that the “correction formula of Peirce and Cellérier is suited perfectly to practice and represents exactly the variation of period caused by swaying of the support, on the condition that one uses the statical coefficient.” Defforges developed a theory for the employment of two similar pendulums of the same weight, but of different length, and hung by the same knives. This theory eliminated the flexure of the support and the curvature of the knives from the reduction of observations.
Pendulums of 1-meter and of 1/2-meter distance between the knife edges were constructed from Defforges’ design by Brunner Brothers in Paris (fig. 21). These Defforges pendulums were cylindrical in form with hemispherical ends like the Peirce pendulums, and were hung on knives that projected from the sides of the pendulum, as in some unfinished Gautier pendulums designed by Peirce in 1883 in Paris.[Pg 330]
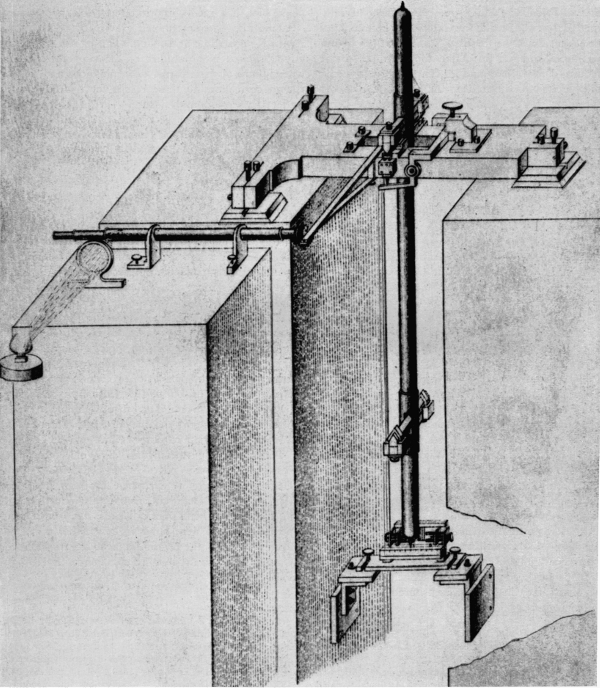
Figure 21.—Reversible pendulum apparatus of Defforges, as constructed by Brunner, Paris, about 1887. The clock and telescope used to observe coincidences are not shown. The telescope shown is part of an interferometer used to measure flexure of the support. One mirror of the interferometer is attached to the pendulum support; the other to the separate masonry pillar at the left.
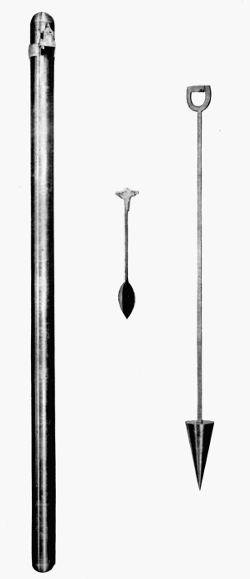
Figure 22.—Because of the greater simplicity of its use, the invariable pendulum superseded the convertible pendulum towards the end of the 19th century, except at various national base stations (Kew, Paris, Potsdam, Washington, D.C., etc.). Shown here are, right to left, a pendulum of the type used by Peirce at the Hoosac Tunnel in 1873-74, the Mendenhall 1/2-second pendulum of 1890, and the pendulum designed by Peirce in 1881-1882.

Figure 23.—The overall size of portable pendulum apparatus was greatly reduced with the introduction of this 1/2-second apparatus in 1887, by the Austrian military officer, Robert von Sterneck. Used with a vacuum chamber not shown here, the apparatus is only about 2 feet high. Coincidences are observed by the reflection of a periodic electric spark in two mirrors, one on the support and the other on the pendulum itself.

Figure 24.—Thomas C. Mendenhall (1841-1924). Although largely self-educated, he became the first professor of physics and mechanics at the Ohio Agricultural and Mechanical College (later Ohio State University), and was subsequently connected with several other universities. In 1878, while teaching at the Tokyo Imperial University in Japan, he made gravity measurements between Tokyo and Fujiyama from which he calculated the mean density of the earth. While superintendent of the U.S. Coast and Geodetic Survey, 1889-94, he developed the pendulum apparatus which bears his name.
Von Sterneck and Mendenhall Pendulums
While scientists who had used the Repsold-Bessel pendulum apparatus discussed its defects and limitations for gravity surveys, Maj. Robert von Sterneck of Austria-Hungary began to develop an excellent apparatus for the rapid determination of relative values of gravity.[82] Maj. von Sterneck’s apparatus contained a nonreversible pendulum 1/4-meter in[Pg 332] length, and 1/2-second time of swing. The pendulum was hung by a single knife edge, which rested on a plate that was supported by a tripod. The pendulum was swung in a chamber from which air was exhausted and which could be maintained at any desired temperature. Times of swing were determined by the observation of coincidences of the pendulum with chronometer signals. In the final form a small mirror was attached to the knife edge perpendicular to the plane of vibration of the pendulum and a second fixed mirror was placed close to it so that the two mirrors were parallel when the pendulum was at rest. The chronometer signals worked a relay that gave a horizontal spark which was reflected into the telescope from the mirrors. When the pendulum was at rest, the image of the spark in both mirrors appeared on the horizontal cross wire in the telescope, and during oscillation of the pendulum the two images appeared in that position upon coincidence. In view of the reduced size of the pendulum, the chamber in which it was swung was readily portable, and with an improved method of observing coincidences, relative determinations of gravity could be made with rapidity and accuracy.
By 1887 Maj. von Sterneck had perfected his apparatus, and it was widely adopted in Europe for relative determinations of gravity. He used his apparatus in extensive gravity surveys and also applied it in the silver mines in Saxony and Bohemia, by the previously described methods of Airy, for investigations into the internal constitution of the earth.
On July 1, 1889, Thomas Corwin Mendenhall became superintendent of the U.S. Coast and Geodetic Survey. Earlier, he had been professor of physics at the University of Tokyo and had directed observations of pendulums for the determination of gravity on Fujiyama and at Tokyo. Supt. Mendenhall, with the cooperation of members of his staff in Washington, designed a new pendulum apparatus of the von Sterneck type, and in October 1890 he ordered construction of the first model.[83]
Like the Von Sterneck apparatus, the Mendenhall pendulum apparatus employed a nonreversible, invariable pendulum 1/4-meter in length and of slightly more than 1/2-second in time of swing. Initially, the knife edge was placed in the head of the pendulum and hung on a fixed plane support, but after some experimentation Mendenhall attached the plane surface to the pendulum and hung it on a fixed knife edge. An apparatus was provided with a set of three pendulums, so that if discrepancies appeared in the results, the pendulum at fault could be detected. There was also a dummy pendulum which carried a thermometer. A pendulum was swung in a receiver in which the pressure and temperature of the air were controlled. The time of swing was measured by coincidences with the beat of a chronometer. The coincidences were determined by an optical method with the aid of a flash apparatus.[Pg 333]

Figure 25.—Mendenhall’s 1/4-meter (1/2-second) apparatus. Shown on the left is the flash apparatus and, on the right, the vacuum chamber within which the pendulum is swung. The flash apparatus consists of a kerosene lantern and a telescope, mounted on a box containing an electromagnetically operated shutter. The operation of the shutter is controlled by a chronograph (not shown), so that it emits a slit of light at regular intervals. The telescope is focused on two mirrors within the apparatus, one fixed, the other attached to the top of the pendulum. It is used to observe the reflection of the flashes from these mirrors. When the two reflections are aligned, a “coincidence” is marked on the chronograph tape. The second telescope attached to the bottom of the vacuum chamber is for observing the amplitude of the pendulum swing.
The flash apparatus was contained in a light metal box which supported an observing telescope and which was mounted on a stand. Within the box was an electromagnet whose coils were connected with a chronometer circuit and whose armature carried a long arm that moved two shutters, in both of which were horizontal slits of the same size. The shutters were behind the front face of the box, which also had a horizontal slit. A flash of light from an oil lamp or an electric spark was emitted from the box when the circuit was broken, but not when it was closed. When the circuit was broken a spring caused the arm to rise, and the shutters were actuated so that the three slits came into line and a flash of light was emitted. A small circular mirror was set in each side of the pendulum head, so that from either face of the pendulum the image of the illuminated slit could be reflected into the field of the observing telescope. A similar mirror was placed parallel to these two mirrors and rigidly attached to the support. The chronometer signals broke the circuit, causing the three slits momentarily to be in line, and when the images of the slit in the two mirrors coincided, a coincidence was observed. A coincidence occurred whenever the pendulum gained or lost one oscillation on the beat[Pg 334] of the chronometer. The relative intensity of gravity was determined by observations with the first Mendenhall apparatus at Washington, D.C., at stations on the Pacific Coast and in Alaska, and at the Stevens Institute, Hoboken, New Jersey, between March and October 1891.
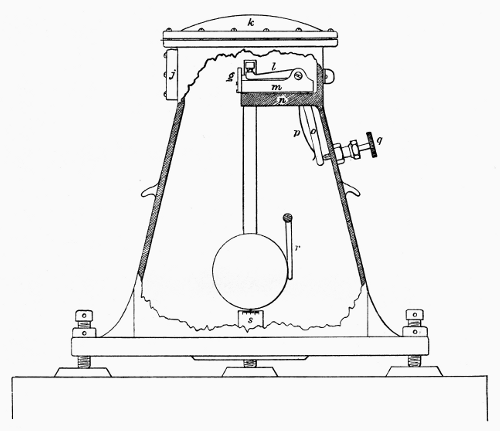
Figure 26.—Vacuum receiver within which the Mendenhall pendulum is swung. The pressure is reduced to about 50 mm. to reduce the disturbing effect of air resistance. When the apparatus is sealed, the pendulum is lifted on the knife edge by the lever q and is started to swing by the lever r. The arc of swing is only about 1°. The stationary mirror is shown at g. The pendulum shown in outline in the center, is only about 9.7 inches long.
Under Supt. Mendenhall’s direction a smaller, 1/4-second, pendulum apparatus was also constructed and tested, but did not offer advantages over the 1/2-second apparatus, which therefore continued in use.
In accordance with Peirce’s theory of the flexure of the stand under oscillations of the pendulum, determinations of the displacement of the receiver of the Mendenhall apparatus were part of a relative determination of gravity by members of the Coast and Geodetic Survey. Initially, a statical method was used, but during 1908-1909 members of the Survey adapted the Michelson interferometer for the determinations of flexure during oscillations from the shift of fringes.[84] The first Mendenhall pendulums were made of bronze, but about 1920 invar was chosen because of its small coefficient of expansion. About 1930, Lt. E. J. Brown of the Coast and Geodetic Survey made significant improvements in the Mendenhall apparatus, and the new form came to be known as the Brown Pendulum Apparatus.[85][Pg 335]

Figure 27.—The Michelson interferometer. The horizontal component of the force acting on the knife edge through the swinging pendulum causes the support to move in unison with the pendulum, and thereby affects the period of the oscillation. This movement is the so-called flexure of the pendulum support, and must be taken into account in the most accurate observations.
In 1907, the Michelson interferometer was adapted to this purpose by the U.S. Coast and Geodetic Survey. As shown here, the interferometer, resting on a wooden beam, is introduced into the path of a light beam reflected from a mirror on the vacuum chamber. Movement of that mirror causes a corresponding movement in the interference fringes in the interferometer, which can be measured.
The original Von Sterneck apparatus and that of Mendenhall provided for the oscillation of one pendulum at a time. After the adoption of the Von Sterneck pendulum in Europe, there were developed stands on which two or four pendulums hung at the same time. This procedure provided a convenient way to observe more than one invariable pendulum at a station for the purpose of detecting changes in length. Prof. M. Haid of Karlsruhe in 1896 described a four-pendulum apparatus,[86] and Dr. Schumann of Potsdam subsequently described a two-pendulum apparatus.[87][Pg 336]

Figure 28.—Apparatus which was developed in 1929 by the Gulf Research and Development Company, Harmarville, Pennsylvania. It was designed to achieve an accuracy within one ten-millionth of the true value of gravity, and represents the extreme development of pendulum apparatus for relative gravity measurement. The pendulum was designed so that the period would be a minimum. The case (the top is missing in this photograph) is dehumidified and its temperature and electrostatic condition are controlled. Specially designed pendulum-lifting and -starting mechanisms are used. The problem of flexure of the case is overcome by the Faye-Peirce method (see text) in which two dynamically matched pendulums are swung simultaneously, 180° apart in phase.
The multiple-pendulum apparatus then provided a method of determining the flexure of the stand from the action of one pendulum upon a second pendulum hung on the same stand. This method of determining the correction for flexure was a development from a “Wippverfahren” invented at the Geodetic Institute in Potsdam. A dynamometer was used to impart periodic impulses to the stand, and the effect was observed upon a pendulum initially at rest. Refinements of this method led to the development of a method used by Lorenzoni in 1885-1886 to determine the flexure of the stand by action of an auxiliary pendulum upon the principal pendulum. Dr. Schumann, in 1899, gave a mathematical theory of such determinations,[88] and in his paper cited the mathematical methods of Peirce and Cellérier for the theory of Faye’s proposal at Stuttgart in 1877 to swing two similar pendulums on the same support with equal amplitudes and in opposite phases.[Pg 337]

Figure 29.—The Gulf pendulum is about 10.7 inches long, and has a period of .89 second. It is made of fused quartz which is resistant to the influence of temperature change and to the earth’s magnetism. Quartz pendulums are subject to the influence of electrostatic charge, and provision is made to counteract this through the presence of a radium salt in the case. The bearings are made of Pyrex glass.
In 1902, Dr. P. Furtwängler[89] presented the mathematical theory of coupled pendulums in a paper in which he referred to Faye’s proposal of 1877 and reported that the difficulties predicted upon its application had been found not to occur. Finally, during the gravity survey of Holland in the years 1913-1921, in view of instability of supports caused by the mobility of the soil, F. A. Vening Meinesz adopted Faye’s proposed method of swinging two pendulums on the same support.[90] The observations were made with the ordinary Stückrath apparatus, in which four Von Sterneck pendulums swung two by two in planes perpendicular to each other. This successful application of the method—which had been proposed by Faye and had been demonstrated theoretically to be sound by Peirce, who also published a design for its[Pg 338] application—was rapidly followed for pendulum apparatus for relative determinations by Potsdam,[91] Cambridge (England),[92] Gulf Oil and Development Company,[93] and the Dominion Observatory at Ottawa.[94] Heiskanen and Vening Meinesz state:
The best way to eliminate the effect of flexure is to use two synchronized pendulums of the same length swinging on the same apparatus in the same plane and with the same amplitudes but in opposite phases; it is clear then the flexure is zero.[95]
In view of the fact that the symmetrical reversible pendulum is named for Bessel, who created the theory and a design for its application by Repsold, it appears appropriate to call the method of eliminating flexure by swinging two pendulums on the same support the Faye-Peirce method. Its successful application was made possible by Maj. von Sterneck’s invention of the short, 1/4-meter pendulum.
Figure 30.—The accumulated data of gravity observations over the earth’s surface have indicated that irregularities such as mountains do not have the effect which would be expected in modifying gravity, but are somehow compensated for. The most satisfactory solution to this still unanswered question has been the theory of isostasy, according to which variations in the density of the material in the earth’s crust produce a kind of hydrostatic equilibrium between its higher and lower parts, as they “float” on the earth’s fluid core. The metals of different density floating in mercury in this diagram illustrate isostasy according to the theory of Pratt and Hayford.
Absolute Value of Gravity at Potsdam
The development of the reversible pendulum in the 19th century culminated in the absolute determination of the intensity of gravity at Potsdam by Kühnen and Furtwängler of the Royal Prussian Geodetic Institute, which then became the world base for gravity surveys.[96]
We have previously seen that in 1869 the Geodetic Institute—founded by Lt. Gen. Baeyer—had acquired a Repsold-Bessel reversible pendulum which was swung by Dr. Albrecht under the direction of Dr. Bruhns. Dissatisfaction with this instrument was expressed by Baeyer in 1875 to Charles S. Peirce, who then, by experiment and mathematical analysis of the flexure of the stand under oscillations of the pendulum, determined that previously reported results with the Repsold apparatus required correction. Dr. F. R. Helmert, who in 1887 succeeded Baeyer as director of the Institute, secured construction of a building for the Institute in Potsdam, and under his direction the scientific study of the intensity of gravity was pursued with vigor. In 1894, it was discovered in Potsdam that a pendulum constructed of very flexible material yielded results which differed markedly from those obtained with pendulums of[Pg 339] greater stiffness. Dr. Kühnen of the Institute discovered that the departure from expectations was the result of the flexure of the pendulum staff itself during oscillations.[97]
Peirce, in 1883, had discovered that the recesses cut in his pendulums for the insertion of tongues that carried the knives had resulted in the flexure of the pendulum staff.[98] By experiment, he also found an even greater flexure for the Repsold pendulum. In order to eliminate this source of error, Peirce designed a pendulum with knives that extended from each side of the cylindrical staff, and he received authorization from the superintendent of the Coast and Geodetic Survey to arrange for the construction of such pendulums by Gautier in Paris. Peirce, who had made his plans in consultation with Gautier, was called home before the pendulums were completed, and these new instruments remained undelivered.
In a memoir titled “Effect of the flexure of a pendulum upon its period of oscillation,”[99] Peirce determined analytically the effect on the period of a pendulum with a single elastic connection between two rigid parts of the staff. Thus, Peirce discovered experimentally the flexure of the staff and derived for a simplified case the effect on the period. It is not known if he ever found the integrated effect of the continuum of elastic connections in the pendulum. Lorenzoni, in 1896, offered a solution to the problem, and Almansi, in 1899, gave an extended analysis. After the independent discovery of the problem at the Geodetic Institute, Dr. Helmert took up the problem and criticized the theories of Peirce and Lorenzoni. He then presented his own theory of flexure in a comprehensive memoir.[100] In view of the previous neglect of the flexure of the pendulum staff in the reduction of observations, Helmert directed that the Geodetic Institute make a new absolute determination of the intensity of gravity at Potsdam. For this purpose, Kühnen and Furtwängler used the following reversible pendulums which had been constructed by the firm of A. Repsold and Sons in Hamburg:
1. The seconds pendulum of the Geodetic Institute procured in 1869.
2. A seconds pendulum from the Astronomical Observatory, Padua.
3. A heavy, seconds pendulum from the Imperial and Royal Military-Geographical Institute, Vienna.
4. A light, seconds pendulum from the Imperial and Royal Military-Geographical Institute.
5. A 1/2-second, reversible pendulum of the Geodetic Institute procured in 1892.
Work was begun in 1898, and in 1906 Kühnen and Furtwängler published their monumental memoir, “Bestimmung der Absoluten Grösze der Schwerkraft zu Potsdam mit Reversionspendeln.”
The acceleration of gravity in the pendulum room of the Geodetic Institute was determined to be 981.274 ± 0.003 cm/sec2. In view of the exceptionally careful and thorough determination at the Institute, Potsdam was accepted as the world base for the absolute value of the intensity of gravity. The absolute value of gravity at some other station on the Potsdam system was determined from the times of swing of an invariable pendulum at the station and at Potsdam by the relation T12/T22 = g2/g1. Thus, in 1900, Assistant G. R. Putnam of the Coast and Geodetic Survey swung Mendenhall pendulums at the Washington base and at Potsdam, and by transfer from Potsdam determined the intensity of gravity at the Washington base to be 980.112 cm/sec2.[101] In 1933, Lt. E. J. Brown made comparative measurements with improved apparatus and raised the value at the Washington base to 980.118 cm/sec2.[102]
In view of discrepancies between the results of various relative determinations, the Coast and Geodetic Survey in 1928 requested the National Bureau of Standards to make an absolute determination for Washington. Heyl and Cook used reversible pendulums made of fused silica having a period of approximately 1 second. Their result, published in 1936, was interpreted to indicate that the value at Potsdam was too high by 20 parts in 1 million.[103] This estimate was lowered slightly by Sir Harold Jeffreys of Cambridge, England, who recomputed the results of Heyl and Cook by different methods.[104][Pg 340]
Figure 31.—Map showing the distribution of gravity stations throughout the United States as of December 1908.
[Pg 342] In 1939, J. S. Clark published the results of a determination of gravity with pendulums of a non-ferrous Y-alloy[105] at the National Physical Laboratory at Teddington, England, and, after recomputation of results by Jeffreys, the value was found to be 12.8 parts in 1 million less than the value obtained by transfer from Potsdam. Dr. Hugh L. Dryden of the National Bureau of Standards, and Dr. A. Berroth of the Geodetic Institute at Potsdam, have recomputed the Potsdam data by different methods of adjustment and concluded that the Potsdam value was too high by about 12 parts in a million.[106] Determination of gravity at Leningrad by Russian scientists likewise has indicated that the 1906 Potsdam value is too high. In the light of present information, it appears justifiable to reduce the Potsdam value of 981.274 by .013 cm/sec2 for purposes of comparison. If the Brown transfer from Potsdam in 1933 was taken as accurate, the value for the Washington base would be 980.105 cm/sec2. In this connection, it is of interest to note that the value given by Charles S. Peirce for the comparable Smithsonian base in Washington, as determined by him from comparative methods in the 1880’s and reported in the Annual Report of the Superintendent of the Coast and Geodetic Survey for the year 1890-1891, was 980.1017 cm/sec2.[107] This value would appear to indicate that Peirce’s pendulums, observations, and methods of reduction of data were not inferior to those of the scientists of the Royal Prussian Geodetic Institute at Potsdam.
Doubts concerning the accuracy of the Potsdam value of gravity have stimulated many new determinations of the intensity of gravity since the end of World War II. In a paper published in June 1957, A. H. Cook, Metrology Division, National Physical Laboratory, Teddington, England, stated:
At present about a dozen new absolute determinations are in progress or are being planned. Heyl and Cook’s reversible pendulum apparatus is in use in Buenos Aires and further reversible pendulum experiments have been made in the All Union Scientific Research Institute of Metrology, Leningrad (V N I I M) and are planned at Potsdam. A method using a very long pendulum was tried out in Russia about 1910 and again more recently and there are plans for similar work in Finland. The first experiment with a freely falling body was that carried out by Volet who photographed a graduated scale falling in an enclosure at low air pressure. Similar experiments have been completed in Leningrad and are in progress at the Physikalisch-Technische Bundesanstalt (Brunswick) and at the National Research Council (Ottawa), and analogous experiments are being prepared at the National Physical Laboratory and at the National Bureau of Standards. Finally, Professor Medi, Director of the Istituto Nazionale di Geofisica (Rome), is attempting to measure the focal length of the paraboloidal surface of a liquid in a rotating dish.[108]
Application of Gravity Surveys
We have noted previously that in the ancient and early modern periods, the earth was presupposed to be spherical in form. Determination of the figure of the earth consisted in the measurement of the radius by the astronomical-geodetic method invented by Eratosthenes. Since the earth was assumed to be spherical, gravity was inferred to be constant over the surface of the earth. This conclusion appeared to be confirmed by the determination of the length of the seconds pendulum at various stations in Europe by Picard and others. The observations of Richer in South America, the theoretical discussions of Newton and Huygens, and the measurements of degrees of latitude in Peru and Sweden demonstrated that the earth is an oblate spheroid.

Figure 33.—Gravity characteristics of the globe. Deductions as to the distribution of matter in the earth can be made from gravity measurements. This globe shows worldwide variations in gravity as they now appear from observations at sea (in submarines) as well as on land. It is based on data from the Institute of Geodesy at Ohio State University.
The theory of gravitation and the theory of central forces led to the result that the intensity of gravity is variable over the surface of the earth. Accordingly,[Pg 343] determinations of the intensity of gravity became of value to the geodesist as a means of determining the figure of the earth. Newton, on the basis of the meager data available to him, calculated the ellipticity of the earth to be 1/230 (the ellipticity is defined by (a-b)/a, where a is the equatorial radius and b the polar radius). Observations of the intensity of gravity were made on the historic missions to Peru and Sweden. Bouguer and La Condamine found that at the equator at sea level the seconds pendulum was 1.26 Paris-lines shorter than at Paris. Maupertuis found that in northern Sweden a certain pendulum clock gained 59.1 seconds per day on its rate in Paris. Then Clairaut, from the assumption that the earth is a spheroid of equilibrium, derived a theorem from which the ellipticity of the earth can be derived from values of the intensity of gravity.[Pg 344]

Figure 34.—An exhibit of gravity apparatus at the Smithsonian Institution. Suspended on the wall, from left to right, are the invariable pendulums of Mendenhall (1/2-second), Peirce (1873-1874), and Peirce (1881-1882); the double pendulum of Edward Kübel (see fig. 15, p. 319), and the reversible pendulum of Peirce. On the display counter, from left to right, are the vacuum chamber, telescope and flash apparatus for the Mendenhall 1/4-second apparatus. Shown below these are the four pendulums used with the Mendenhall apparatus, the one on the right having a thermometer attached. At bottom, right, is the Gulf apparatus (cover removed) mentioned in the text, shown with one quartz pendulum.
[Pg 345] Early in the 19th century a systematic series of observations began to be conducted in order to determine the intensity of gravity at stations all over the world. Kater invariable pendulums, of which 13 examples have been mentioned in the literature, were used in surveys of gravity by Kater, Sabine, Goldingham, and other British pendulum swingers. As has been noted previously, a Kater invariable pendulum was used by Adm. Lütke of Russia on a trip around the world. The French also sent out expeditions to determine values of gravity. After several decades of relative inactivity, Capts. Basevi and Heaviside of the Indian Survey carried out an important series of observations from 1865 to 1873 with Kater invariable pendulums and the Russian Repsold-Bessel pendulums. In 1881-1882 Maj. J. Herschel swung Kater invariable pendulums nos. 4, 6 (1821), and 11 at stations in England and then brought them to the United States in order to make observations which would connect American and English base stations.[109]
The extensive sets of observations of gravity provided the basis of calculations of the ellipticity of the earth. Col. A. R. Clarke in his Geodesy (London, 1880) calculated the ellipticity from the results of gravity surveys to be 1/(292.2 ± 1.5). Of interest is the calculation by Charles S. Peirce, who used only determinations made with Kater invariable pendulums and corrected for elevation, atmospheric effect, and expansion of the pendulum through temperature.[110] He calculated the ellipticity of the earth to be 1/(291.5 ± 0.9).
The 19th century witnessed the culmination of the ellipsoidal era of geodesy, but the rapid accumulation of data made possible a better approximation to the figure of the earth by the geoid. The geoid is defined as the average level of the sea, which is thought of as extended through the continents. The basis of geodetic calculations, however, is an ellipsoid of reference for which a gravity formula expresses the value of normal gravity at a point on the ellipsoid as a function of gravity at sea level at the equator, and of latitude. The general assembly of the International Union of Geodesy and Geophysics, which was founded after World War I to continue the work of Die Internationale Erdmessung, adopted in 1924 an international reference ellipsoid,[111] of which the ellipticity, or flattening, is Hayford’s value 1/297. In 1930, the general assembly adopted a correlated International Gravity Formula of the form γ = γE(1 + β(sin2 φ) + ε(sin2 2φ)) where γ is normal gravity at latitude φ, γE is the value of gravity at sea level at the equator, β is a parameter which is computed on the basis of Clairaut’s theorem from the flattening value of the meridian, and ε is a constant which is derived theoretically. The plumb line is perpendicular to the geoid, and the components of angle between the perpendiculars to geoid and reference ellipsoid are deflections of the vertical. The geoid is above the ellipsoid of reference under mountains and it is below the ellipsoid on the oceans, where the geoid coincides with mean sea level. In physical geodesy, gravimetric data are used for the determination of the geoid and components of deflections of the vertical. For this purpose, one must reduce observed values of gravity to sea level by various reductions, such as free-air, Bouguer, isostatic reductions. If g0 is observed gravity reduced to sea level and γ is normal gravity obtained from the International Gravity Formula, then Δg = g0 - γ is the gravity anomaly.[112]
In 1849, Stokes derived a theorem whereby the distance N of the geoid from the ellipsoid of reference can be obtained from an integration of gravity anomalies over the surface of the earth. Vening Meinesz further derived formulae for the calculation of components of the deflection of the vertical.
Geometrical geodesy, which was based on astronomical-geodetic methods, could give information only concerning the external form of the figure of the earth. The gravimetric methods of physical geodesy, in conjunction with methods such as those of seismology, enable scientists to test hypotheses concerning the internal structure of the earth. Heiskanen and Vening Meinesz summarize the present-day achievements of the gravimetric method of[Pg 346] physical geodesy by stating[113] that it alone can give:
1. The flattening of the reference ellipsoid.
2. The undulations N of the geoid.
3. The components of the deflection of the vertical ζ and η at any point, oceans and islands included.
4. The conversion of existing geodetic systems to the same world geodetic system.
5. The reduction of triangulation base lines from the geoid to the reference ellipsoid.
6. The correction of errors in triangulation in mountainous regions due to the effect of the deflections of the vertical.
7. Geophysical applications of gravity measurements, e.g., the isostatic study of the earth’s interior and the exploration of oil fields and ore deposits.
With astronomical observations or with existing triangulations, the gravimetric method can accomplish further results. Heiskanen and Vening Meinesz state:
It is the firm conviction of the authors that the gravimetric method is by far the best of the existing methods for solving the main problems of geodesy, i.e., to determine the shape of the geoid on the continents as well as at sea and to convert the existing geodetic systems to the world geodetic system. It can also give invaluable help in the computation of the reference ellipsoid.[114]
Summary
Since the creation of classical mechanics in the 17th century, the pendulum has been a basic instrument for the determination of the intensity of gravity, which is expressed as the acceleration of a freely falling body. Basis of theory is the simple pendulum, whose time of swing under gravity is proportional to the square root of the length divided by the acceleration due to gravity. Since the length of a simple pendulum divided by the square of its time of swing is equal to the length of a pendulum that beats seconds, the intensity of gravity also has been expressed in terms of the length of the seconds pendulum. The reversible compound pendulum has served for the absolute determination of gravity by means of a theory developed by Huygens. Invariable compound pendulums with single axes also have been used to determine relative values of gravity by comparative times of swing.
The history of gravity pendulums begins with the ball or “simple” pendulum of Galileo as an approximation to the ideal simple pendulum. Determinations of the length of the seconds pendulum by French scientists culminated in a historic determination at Paris by Borda and Cassini, from the corrected observations with a long ball pendulum. In the 19th century, Bessel found the length of the seconds pendulum at Königsberg and Berlin by observations with a ball pendulum and by original theoretical considerations. During the century, however, the compound pendulum came to be preferred for absolute and relative determinations.
Capt. Henry Kater, at London, constructed the first convertible compound for an absolute determination of gravity, and then he designed an invariable compound pendulum, examples of which were used for relative determinations at various stations in Europe and elsewhere. Bessel demonstrated theoretically the advantages of a reversible compound pendulum which is symmetrical in form and is hung by interchangeable knives. The firm of A. Repsold and Sons in Hamburg constructed pendulums from the specifications of Bessel for European gravity surveys.
Charles S. Peirce in 1875 received delivery in Hamburg of a Repsold-Bessel pendulum for the U.S. Coast Survey and observed with it in Geneva, Paris, Berlin, and London. Upon an initial stimulation from Baeyer, founder of Die Europäische Gradmessung, Peirce demonstrated by experiment and theory that results previously obtained with the Repsold apparatus required correction, because of the flexure of the stand under oscillations of the pendulum. At the Stuttgart conference of the geodetic association in 1877, Hervé Faye proposed to solve the problem of flexure by swinging two similar pendulums from the same support with equal amplitudes and in opposite phases. Peirce, in 1879, demonstrated theoretically the soundness of the method and presented a design for its application, but the “double pendulum” was rejected at that time. Peirce also designed and had constructed four examples of a new type of invariable, reversible pendulum of cylindrical form which made possible the experimental study of Stokes’ theory of the resistance to motion of a pendulum in a viscous fluid. Commandant Defforges, of France, also designed and used cylindrical reversible pendulums, but of different length so that the effect of flexure was eliminated in the reduction of observations. Maj. Robert von Sterneck, of Austria-Hungary, initiated a new era in gravity research by the invention of an apparatus with a short pendulum for relative determinations of gravity. Stands were then constructed in Europe on[Pg 347] which two or four pendulums were hung at the same time. Finally, early in the present century, Vening Meinesz found that the Faye-Peirce method of swinging pendulums hung on a Stückrath four-pendulum stand solved the problem of instability due to the mobility of the soil in Holland.
The 20th century has witnessed increasing activity in the determination of absolute and relative values of gravity. Gravimeters have been perfected and have been widely used for rapid relative determinations, but the compound pendulums remain as indispensable instruments. Mendenhall’s replacement of knives by planes attached to nonreversible pendulums has been used also for reversible ones. The Geodetic Institute at Potsdam is presently applying the Faye-Peirce method to the reversible pendulum.[115] Pendulums have been constructed of new materials, such as invar, fused silica, and fused quartz. Minimum pendulums for precise relative determinations have been constructed and used. Reversible pendulums have been made with “I” cross sections for better stiffness. With all these modifications, however, the foundations of the present designs of compound pendulum apparatus were created in the 19th century.
FOOTNOTES:
[1] The basic historical documents have been collected, with a bibliography of works and memoirs published from 1629 to the end of 1885, in Collection de mémoires relatifs a la physique, publiés par la Société française de Physique [hereinafter referred to as Collection de mémoires]: vol. 4, Mémoires sur le pendule, précédés d’une bibliographie (Paris: Gauthier-Villars, 1889); and vol. 5, Mémoires sur le pendule, part 2 (Paris: Gauthier-Villars, 1891). Important secondary sources are: C. Wolf, “Introduction historique,” pp. 1-42 in vol. 4, above; and George Biddell Airy, “Figure of the Earth,” pp. 165-240 in vol. 5 of Encyclopaedia metropolitana (London, 1845).
[2] Galileo Galilei’s principal statements concerning the pendulum occur in his Discourses Concerning Two New Sciences, transl. from Italian and Latin into English by Henry Crew and Alfonso de Salvio (Evanston: Northwestern University Press, 1939), pp. 95-97, 170-172.
[3] P. Marin Mersenne, Cogitata physico-mathematica (Paris, 1644), p. 44.
[4] Christiaan Huygens, Horologium oscillatorium, sive de motu pendulorum ad horologia adaptato demonstrationes geometricae (Paris, 1673), proposition 20.
[5] The historical events reported in the present section are from Airy, “Figure of the Earth.”
[6] Abbé Jean Picard, La Mesure de la terre (Paris, 1671). John W. Olmsted, “The ‘Application’ of Telescopes to Astronomical Instruments, 1667-1669,” Isis (1949), vol. 40, p. 213.
[7] The toise as a unit of length was 6 Paris feet or about 1,949 millimeters.
[8] Jean Richer, Observations astronomiques et physiques faites en l’isle de Caïenne (Paris, 1679). John W. Olmsted, “The Expedition of Jean Richer to Cayenne 1672-1673,” Isis (1942), vol. 34, pp. 117-128.
[9] The Paris foot was 1.066 English feet, and there were 12 lines to the inch.
[10] Christiaan Huygens, “De la cause de la pesanteur,” Divers ouvrages de mathematiques et de physique par MM. de l’Académie Royale des Sciences (Paris, 1693), p. 305.
[11] Isaac Newton, Philosophiae naturalis principia mathematica (London, 1687), vol. 3, propositions 18-20.
[12] Pierre Bouguer, La figure de la terre, déterminée par les observations de Messieurs Bouguer et de La Condamine, envoyés par ordre du Roy au Pérou, pour observer aux environs de l’equateur (Paris, 1749).
[13] P. L. Moreau de Maupertuis, La figure de la terre déterminée par les observations de Messieurs de Maupertuis, Clairaut, Camus, Le Monnier, l’Abbé Outhier et Celsius, faites par ordre du Roy au cercle polaire (Paris, 1738).
[14] Paris, 1743.
[15] George Gabriel Stokes, “On Attraction and on Clairaut’s Theorem,” Cambridge and Dublin Mathematical Journal (1849), vol. 4, p. 194.
[16] See Collection de mémoires, vol. 4, p. B-34, and J. H. Poynting and Sir J. J. Thomson, Properties of Matter (London, 1927), p. 24.
[17] Poynting and Thomson, ibid., p. 22.
[18] Charles M. de la Condamine, “De la mesure du pendule à Saint Domingue,” Collection de mémoires, vol. 4, pp. 3-16.
[19] Père R. J. Boscovich, Opera pertinentia ad Opticam et Astronomiam (Bassani, 1785), vol. 5, no. 3.
[20] J. C. Borda and J. D. Cassini de Thury, “Expériences pour connaître la longueur du pendule qui bat les secondes à Paris,” Collection de mémoires, vol. 4, pp. 17-64.
[21] F. W. Bessel, “Untersuchungen über die Länge des einfachen Secundenpendels,” Abhandlungen der Königlichen Akademie der Wissenschaften zu Berlin, 1826 (Berlin, 1828).
[22] Bessel used as a standard of length a toise which had been made by Fortin in Paris and had been compared with the original of the “toise de Peru” by Arago.
[23] L. G. du Buat, Principes d’hydraulique (Paris, 1786). See excerpts in Collection de mémoires, pp. B-64 to B-67.
[24] Capt. Henry Kater, “An Account of Experiments for Determining the Length of the Pendulum Vibrating Seconds in the Latitude of London,” Philosophical Transactions of the Royal Society of London (1818), vol. 108, p. 33. [Hereinafter abbreviated Phil. Trans.]
[25] M. G. de Prony, “Méthode pour déterminer la longueur du pendule simple qui bat les secondes,” Collection de mémoires, vol. 4, pp. 65-76.
[26] Collection de mémoires, vol. 4, p. B-74.
[27] Phil. Trans. (1819), vol. 109, p. 337.
[28] John Herschel, “Notes for a History of the Use of Invariable Pendulums,” The Great Trigonometrical Survey of India (Calcutta, 1879), vol. 5.
[29] Capt. Edward Sabine, “An Account of Experiments to Determine the Figure of the Earth,” Phil. Trans. (1828), vol. 118, p. 76.
[30] John Goldingham, “Observations for Ascertaining the Length of the Pendulum at Madras in the East Indies,” Phil. Trans. (1822), vol. 112, p. 127.
[31] Basil Hall, “Letter to Captain Kater Communicating the Details of Experiments made by him and Mr. Henry Foster with an Invariable Pendulum,” Phil. Trans. (1823), vol. 113, p. 211.
[32] See Collection de mémoires, vol. 4, p. B-103.
[33] Ibid., p. B-88.
[34] Ibid., p. B-94.
[35] Francis Baily, “On the Correction of a Pendulum for the Reduction to a Vacuum, Together with Remarks on Some Anomalies Observed in Pendulum Experiments,” Phil. Trans. (1832), vol. 122, pp. 399-492. See also Collection de mémoires, vol. 4, pp. B-105, B-112, B-115, B-116, and B-117.
[36] One was of case brass and the other of rolled iron, 68 in. long, 2 in. wide, and 1/2 in. thick. Triangular knife edges 2 in. long were inserted through triangular apertures 19.7 in. from the center towards each end. These pendulums seem not to have survived. There is, however, in the collection of the U.S. National Museum, a similar brass pendulum, 37-5/8 in. long (fig. 15) stamped with the name of Edward Kübel (1820-96), who maintained an instrument business in Washington, D.C., from about 1849. The history of this instrument is unknown.
[37] See Baily’s remarks in the Monthly Notices of the Royal Astronomical Society (1839), vol. 4, pp. 141-143. See also letters mentioned in footnote 38.
[38] This document, together with certain manuscript notes on the pendulum experiments and six letters between Wilkes and Baily, is in the U.S. National Archives, Navy Records Gp. 37. These were the source materials for the information presented here on the Expedition. We are indebted to Miss Doris Ann Esch and Mr. Joseph Rudmann of the staff of the U.S. National Museum for calling our attention to this early American pendulum work.
[39] G. B. Airy, “Account of Experiments Undertaken in the Harton Colliery, for the Purpose of Determining the Mean Density of the Earth,” Phil. Trans. (1856), vol. 146, p. 297.
[40] T. C. Mendenhall, “Measurements of the Force of Gravity at Tokyo, and on the Summit of Fujiyama,” Memoirs of the Science Department, University of Tokyo (1881), no. 5.
[41] J. T. Walker, Account of Operations of The Great Trigonometrical Survey of India (Calcutta, 1879), vol. 5, app. no. 2.
[43] C. A. F. Peters, Briefwechsel zwischen C. F. Gauss und H. C. Schumacher (Altona, Germany, 1860), Band 2, p. 3. The correction required if the times of swing are not exactly the same is said to have been given also by Bohnenberger.
[44] F. W. Bessel, “Construction eines symmetrisch geformten Pendels mit reciproken Axen, von Bessel,” Astronomische Nachrichten (1849), vol. 30, p. 1.
[45] E. Plantamour, “Expériences faites à Genève avec le pendule à réversion,” Mémoires de la Société de Physique et d’histoire naturelle de Genève, 1865 (Geneva, 1866), vol. 18, p. 309.
[46] Ibid., pp. 309-416.
[47] C. Cellérier, “Note sur la Mesure de la Pesanteur par le Pendule,” Mémoires de la Société de Physique et d’histoire naturelle de Genève, 1865 (Geneva, 1866), vol. 18, pp. 197-218.
[48] A. Sawitsch, “Les variations de la pesanteur dans les provinces occidentales de l’Empire russe,” Memoirs of the Royal Astronomical Society (1872), vol. 39, p. 19.
[49] J. J. Baeyer, Über die Grösse und Figur der Erde (Berlin, 1861).
[50] Comptes-rendus de la Conférence Géodésique Internationale réunie à Berlin du 15-22 Octobre 1864 (Neuchâtel, 1865).
[51] Ibid., part III, subpart E.
[52] Bericht über die Verhandlungen der vom 30 September bis 7 October 1867 zu Berlin abgehaltenen allgemeinen Conferenz der Europäischen Gradmessung (Berlin, 1868). See report of fourth session, October 3, 1867.
[53] C. Bruhns and Albrecht, “Bestimmung der Länge des Secundenpendels in Bonn, Leiden und Mannheim,” Astronomisch-Geodätische Arbeiten im Jahre 1870 (Leipzig: Veröffentlichungen des Königlichen Preussischen Geodätischen Instituts, 1871).
[54] Bericht über die Verhandlungen der vom 23 bis 28 September 1874 in Dresden abgehaltenen vierten allgemeinen Conferenz der Europäischen Gradmessung (Berlin, 1875). See report of second session, September 24, 1874.
[55] Carolyn Eisele, “Charles S. Peirce—Nineteenth-Century Man of Science,” Scripta Mathematica (1959), vol 24, p. 305. For the account of the work of Peirce, the authors are greatly indebted to this pioneer paper on Peirce’s work on gravity. It is worth noting that the history of pendulum work in North America goes back to the celebrated Mason and Dixon, who made observations of “the going rate of a clock” at “the forks of the river Brandiwine in Pennsylvania,” in 1766-67. These observations were published in Phil. Trans. (1768), vol. 58, pp. 329-335.
[56] The pendulums with conical bobs are described and illustrated in E. D. Preston, “Determinations of Gravity and the Magnetic Elements in Connection with the United States Scientific Expedition to the West Coast of Africa, 1889-90,” Report of the Superintendent of the Coast and Geodetic Survey for 1889-90 (Washington, 1891), app. no. 12.
[58] The record of Peirce’s observations in Europe during 1875-76 is given in C. S. Peirce, “Measurements of Gravity at Initial Stations in America and Europe,” Report of the Superintendent of the Coast Survey for 1875-76 (Washington, 1879), pp. 202-337 and 410-416. Peirce’s report is dated December 13, 1878, by which time the name of the Survey had been changed to U.S. Coast and Geodetic Survey.
[59] Verhandlungen der vom 20 bis 29 September 1875 in Paris Vereinigten Permanenten Commission der Europäischen Gradmessung (Berlin, 1876).
[60] Ibid. See report for fifth session, September 25, 1875.
[61] The experiments at the Stevens Institute, Hoboken, were reported by Peirce to the Permanent Commission which met in Hamburg, September 4-8, 1878, and his report was published in the general Bericht for 1878 in the Verhandlungen der vom 4 bis 8 September 1878 in Hamburg Vereinigten Permanenten Commission der Europäischen Gradmessung (Berlin, 1879), pp. 116-120. Assistant J. E. Hilgard attended for the U.S. Coast and Geodetic Survey. The experiments are described in detail in C. S. Peirce, “On the Flexure of Pendulum Supports,” Report of the Superintendent of the U.S. Coast and Geodetic Survey for 1880-81 (Washington, 1883), app. no. 14, pp. 359-441.
[62] Verhandlungen der vom 5 bis 10 Oktober 1876 in Brussels Vereinigten Permanenten Commission der Europäischen Gradmessung (Berlin, 1877). See report of third session, October 7, 1876.
[63] Verhandlungen der vom 27 September bis 2 Oktober 1877 zu Stuttgart abgehaltenen fünften allgemeinen Conferenz der Europäischen Gradmessung (Berlin, 1878).
[64] Verhandlung der vom 16 bis 20 September 1879 in Genf Vereinigten Permanenten Commission der Europäischen Gradmessung (Berlin, 1880).
[65] Assistants’ Reports, U.S. Coast and Geodetic Survey, 1879-80. Peirce’s paper was published in the American Journal of Science (1879), vol. 18, p. 112.
[66] Comptes-rendus de l’Académie des Sciences (Paris, 1879), vol. 89, p. 462.
[67] Verhandlungen der vom 13 bis 16 September 1880 zu München abgehaltenen sechsten allgemeinen Conferenz der Europäischen Gradmessung (Berlin, 1881).
[68] Ibid., app. 2.
[69] Ibid., app. 2a.
[70] Verhandlungen der vom 11 bis zum 15 September 1882 im Haag Vereinigten Permanenten Commission der Europäischen Gradmessung (Berlin, 1883).
[71] Verhandlungen der vom 15 bis 24 Oktober 1883 zu Rom abgehaltenen siebenten allgemeinen Conferenz der Europäischen Gradmessung (Berlin, 1884). Gen. Cutts attended for the U.S. Coast and Geodetic Survey.
[72] Ibid., app. 6. See also, Zeitschrift für Instrumentenkunde (1884), vol. 4, pp. 303 and 379.
[74] Report of the Superintendent of the U.S. Coast and Geodetic Survey for 1880-81 (Washington, 1883), p. 26.
[75] Report of the Superintendent of the U.S. Coast and Geodetic Survey for 1889-90 (Washington, 1891), app. no. 12.
[76] Report of the Superintendent of the U.S. Coast and Geodetic Survey for 1881-82 (Washington, 1883).
[77] Transactions of the Cambridge Philosophical Society (1856), vol. 9, part 2, p. 8. Also published in Mathematical and Physical Papers (Cambridge, 1901), vol. 3, p. 1.
[78] Peirce’s comparison of theory and experiment is discussed in a report on the Peirce memoir by William Ferrel, dated October 19, 1890, Martinsburg, West Virginia. U.S. Coast and Geodetic Survey, Special Reports, 1887-1891 (MS, National Archives, Washington).
[79] The stations at which observations were conducted with the Peirce pendulums are recorded in the reports of the Superintendent of the U.S. Coast and Geodetic Survey from 1881 to 1890.
[80] Comptes-rendus de l’Académie des Sciences (Paris, 1880), vol. 90, p. 1401. Hervé Faye’s report, dated June 21, 1880, is in the same Comptes-rendus, p. 1463.
[81] Commandant C. Defforges, “Sur l’Intensité absolue de la pesanteur,” Journal de Physique (1888), vol. 17, pp. 239, 347, 455. See also, Defforges, “Observations du pendule,” Mémorial du Dépôt général de la Guerre (Paris, 1894), vol. 15. In the latter work, Defforges described a pendulum “reversible inversable,” which he declared to be truly invariable and therefore appropriate for relative determinations. The knives remained fixed to the pendulums, and the effect of interchanging knives was obtained by interchanging weights within the pendulum tube.
[82] Papers by Maj. von Sterneck in Mitteilungen des K. u. K. Militär-geographischen Instituts, Wien, 1882-87; see, in particular, vol. 7 (1887).
[83] T. C. Mendenhall, “Determinations of Gravity with the New Half-Second Pendulum ...,” Report of the Superintendent of the U.S. Coast and Geodetic Survey for 1890-91 (Washington, 1892), part 2, pp. 503-564.
[84] W. H. Burger, “The Measurement of the Flexure of Pendulum Supports with the Interferometer,” Report of the Superintendent of the U.S. Coast and Geodetic Survey for 1909-10 (Washington, 1911), app. no. 6.
[85] E. J. Brown, A Determination of the Relative Values of Gravity at Potsdam and Washington (Special Publication No. 204, U.S. Coast and Geodetic Survey; Washington, 1936).
[86] M. Haid, “Neues Pendelstativ,” Zeitschrift für Instrumentenkunde (July 1896), vol. 16, p. 193.
[87] Dr. R. Schumann, “Über eine Methode, das Mitschwingen bei relativen Schweremessungen zu bestimmen,” Zeitschrift für Instrumentenkunde (January 1897), vol. 17, p. 7. The design for the stand is similar to that of Peirce’s of 1879.
[88] Dr. R. Schumann, “Über die Verwendung zweier Pendel auf gemeinsamer Unterlage zur Bestimmung der Mitschwingung,” Zeitschrift für Mathematik und Physik (1899), vol. 44, p. 44.
[89] P. Furtwängler, “Über die Schwingungen zweier Pendel mit annähernd gleicher Schwingungsdauer auf gemeinsamer Unterlage,” Sitzungsberichte der Königlicher Preussischen Akademie der Wissenschaften zu Berlin (Berlin, 1902) pp. 245-253. Peirce investigated the plan of swinging two pendulums on the same stand (Report of the Superintendent of the U.S. Coast and Geodetic Survey for 1880-81, Washington, 1883, p. 26; also in Charles Sanders Peirce, Collected Papers, 6.273). At a conference on gravity held in Washington during May 1882, Peirce again advanced the method of eliminating flexure by hanging two pendulums on one support and oscillating them in antiphase (“Report of a conference on gravity determinations held in Washington, D.C., in May, 1882,” Report of the Superintendent of the U.S. Coast and Geodetic Survey for 1881-82, Washington, 1883, app. no. 22, pp. 503-516).
[90] F. A. Vening Meinesz, Observations de pendule dans les Pays-Bas (Delft, 1923).
[91] A. Berroth, “Schweremessungen mit zwei und vier gleichzeitig auf demselben Stativ schwingenden Pendeln,” Zeitschrift für Geophysik, vol. 1 (1924-25), no. 3, p. 93.
[92] “Pendulum Apparatus for Gravity Determinations,” Engineering (1926), vol. 122, pp. 271-272.
[93] Malcolm W. Gay, “Relative Gravity Measurements Using Precision Pendulum Equipment,” Geophysics (1940), vol. 5, pp. 176-191.
[94] L. G. D. Thompson, “An Improved Bronze Pendulum Apparatus for Relative Gravity Determinations,” [published by] Dominion Observatory (Ottawa, 1959), vol. 21, no. 3, pp. 145-176.
[95] W. A. Heiskanen and F. A. Vening Meinesz, The Earth and its Gravity Field (McGraw: New York, 1958).
[96] F. Kühnen and P. Furtwängler, Bestimmung der Absoluten Grösze der Schwerkraft zu Potsdam mit Reversionspendeln (Berlin: Veröffentlichungen des Königlichen Preussischen Geodätischen Instituts, 1906), new ser., no. 27.
[97] Reported by Dr. F. Kühnen to the fifth session, October 9, 1895, of the Eleventh General Conference, Die Internationale Erdmessung, held in Berlin from September 25 to October 12, 1895. A footnote states that Assistant O. H. Tittmann, who represented the United States, subsequently reported Peirce’s prior discovery of the influence of the flexure of the pendulum itself upon the period (Report of the Superintendent of the U.S. Coast and Geodetic Survey for 1883-84, Washington, 1885, app. 16, pp. 483-485).
[98] Assistants’ Reports, U.S. Coast and Geodetic Survey, 1883-84 (MS, National Archives, Washington).
[99] C. S. Peirce, “Effect of the Flexure of a Pendulum Upon its Period of Oscillation,” Report of the Superintendent of the U.S. Coast and Geodetic Survey for 1883-84 (Washington, 1885), app. no. 16.
[100] F. R. Helmert, Beiträge zur Theorie des Reversionspendels (Potsdam: Veröffentlichungen des Königlichen Preussischen Geodätischen Instituts, 1898).
[101] J. A. Duerksen, Pendulum Gravity Data in the United States (Special Publication No. 244, U.S. Coast and Geodetic Survey; Washington, 1949).
[103] Paul R. Heyl and Guy S. Cook, “The Value of Gravity at Washington,” Journal of Research, National Bureau of Standards (1936), vol. 17, p. 805.
[104] Sir Harold Jeffreys, “The Absolute Value of Gravity,” Monthly Notices of the Royal Astronomical Society, Geophysical Supplement (London, 1949), vol. 5, p. 398.
[105] J. S. Clark, “The Acceleration Due to Gravity,” Phil. Trans. (1939), vol. 238, p. 65.
[106] Hugh L. Dryden, “A Reexamination of the Potsdam Absolute Determination of Gravity,” Journal of Research, National Bureau of Standards (1942), vol. 29, p. 303; and A. Berroth, “Das Fundamentalsystem der Schwere im Lichte neuer Reversionspendelmessungen,” Bulletin Géodésique (1949), no. 12, pp. 183-204.
[108] A. H. Cook, “Recent Developments in the Absolute Measurement of Gravity,” Bulletin Géodésique (June 1, 1957), no. 44, pp. 34-59.
[110] C. S. Peirce, “On the Deduction of the Ellipticity of the Earth, from Pendulum Experiments,” Report of the Superintendent of the U.S. Coast and Geodetic Survey for 1880-81 (Washington, 1883), app. no. 15, pp. 442-456.
[112] Ibid., p. 76.
[113] Ibid., p. 309.
[114] Ibid., p. 310.
[115] K. Reicheneder, “Method of the New Measurements at Potsdam by Means of the Reversible Pendulum,” Bulletin Géodésique (March 1, 1959), no. 51, p.72.
U.S. GOVERNMENT PRINTING OFFICE: 1965
For sale by the Superintendent of Documents, U.S. Government Printing Office
Washington, D.C., 20402—Price 70 cents.
INDEX
Albrecht, Karl Theodore, 322, 338
Al-Mamun, seventh calif of Bagdad, 306
Almansi, Emilio, 339
Aristotle, 306
Baeyer, J. J., 321, 322, 324, 338, 346
Baily, Francis, 317
Basevi, James Palladio, 345
Berroth, A., 342
Bessel, Friedrich Wilhelm, 313, 314, 319, 320, 324, 325, 338, 346
Bohnenberger, Johann Gottlieb Friedrich, 315
Borda, J. C., 311, 312, 315, 325, 329, 346
Boscovitch, Père R. J., 310, 311
Bouguer, Pierre, 307, 309, 327, 343, 345
Brahe, Tycho, 306
Brunner Brothers (Paris), 329
Cassini, Giovanni-Domenico, 306, 307
Cassini, Jacques, 306
Cassini de Thury, J. D., 311, 312, 315, 325, 329, 346
Cellérier, Charles, 320, 321, 325, 326, 329, 336
Clairaut, Alexis Claude, 308, 309, 343, 345
Clark, J. S., 342
Clarke, A. R., 345
Colbert, Jean Baptiste, 306
Cook, A. H., 342
De Freycinet, Louis Claude de Saulses, 317
De la Hire, Gabriel Philippe, 306
De Prony, M. G., 314
Dryden, Hugh L., 342
Du Buat, L. G., 314
Duperry, Capt. Louis Isidore, 317
Eudoxus of Cnidus, 306
Faye, Hervé, 325, 336, 346, 347
Fernel, Jean, 306
Furtwängler, P., 337
Galilei, Galileo, 304, 305, 346
Gauss, C. F., 320
Gautier, P., 339
Godin, Louis, 307
Greely, A. W., 329
Gulf Oil and Development Company, 338
Haid, M., 335
Hall, Basil, 316
Heiskanen, W. A., 338, 345, 346
Helmholtz, Hermann von, 326
Huygens, Christiaan, 304, 305, 307, 314, 342, 346
Ibañez, Carlos, 325
Jeffreys, Sir Harold, 342
Jones, Thomas, 318
Kater, Henry, 304, 314, 325, 327, 329, 345, 346
La Condamine, Charles Marie de, 307, 310, 311, 343
Laplace, Marquis Pierre Simon de, 309, 313, 320
Lütke, Count Feodor Petrovich, 316, 345
Maupertius, P. L. Moreau de, 308, 343
Maxwell, James Clerk, 324
Medi, Enrico, 342
Mendenhall, Thomas Corwin, 319, 331, 332, 334, 347
Mersenne, P. Marin, 305
Newton, Sir Isaac, 303, 307, 308, 342, 343
Norwood, Richard, 306
Oppolzer, Theodor von, 322, 324
Patterson, Carlile Pollock, 325, 326
Peirce, Charles Sanders, 314, 322, 332, 336, 342, 345
Picard, Abbé Jean, 306, 308, 342
Posidonius, 306
Putnam, G. R., 339
Pythagoras, 306
Repsold, A., and Sons (Hamburg), 320, 322, 338, 339, 346
Sabine, Capt. Edward, 315, 325, 329, 345
Schumacher, H. C., 320
Snell, Willebrord, 306
Sterneck, Robert von, 331, 332, 335, 338, 346
Stokes, George Gabriel, 324, 328, 329, 345, 346
Ulloa, Antonio de, 308
Vening Meinesz, F. A., 337, 338, 345
Volet, Charles, 342