- ^ "Restricted Three-Body Problem", Science World.
- ^ "Lagrange Points" by Enrique Zeleny, The Wolfram Demonstrations Project.
- ^ (French) Lagrange, Joseph-Louis (1867-1892). "Tome 6, Chapitre II: Essai sur le problème des trois corps", Oeuvres de Lagrange. Gauthier-Villars, 272-292.
- ^ This apparent contradiction is because the Sun is also affected by the Earth's gravity, and so orbits around the two bodies' barycentre, which is however well inside the body of the Sun.
- ^ Actually
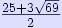
- ^ The Lagrange Points – Neil J. Cornish with input from Jeremy Goodman
- ^ A Search for Natural or Artificial Objects Located at the Earth-Moon Libration Points. Icarus.
- ^ Tyson, Neil deGrasse, Death by Black Hole, ©2007, ISBN 9780393062243
- ^ "Nasa unveils Hubble's successor". BBC (11 May 2007). Retrieved on 2007-11-20.
A contour plot of the effective potential of a two-body system (the Sun and Earth here) as viewed from the rotating frame of reference in which Sun and Earth remain stationary. Objects revolving with the same orbital period as the Earth will begin to move according to the arrows indicating the slopes around the five Lagrange points — downhill toward or away from them, but at the points themselves these forces are balanced. The Lagrangian points ; also Lagrange point, L-point, or libration point), are the five positions in an orbital configuration where a small object affected only by gravity can theoretically be stationary relative to two larger objects (such as a satellite with respect to the Earth and Moon). The Lagrange points mark positions where the combined gravitational pull of the two large masses provides precisely the centripetal force required to rotate with them. They are analogous to geostationary orbits in that they allow an object to be in a "fixed" position in space rather than an orbit in which its relative position changes continuously. A more precise but technical definition is that the Lagrangian points are the stationary solutions of the circular restricted three-body problem [1]. For example, given two massive bodies in circular orbits around their common center of mass, there are five positions in space where a third body, of comparatively negligible mass, could be placed which would then maintain its position relative to the two massive bodies. As seen in a rotating reference frame with the same period as the two co-orbiting bodies, the gravitational fields of two massive bodies combined with the centrifugal force are in balance at the Lagrangian points, allowing the third body to be stationary with respect to the first two bodies.[2] History and concepts In 1772, the Italian-French mathematician Joseph-Louis Lagrange was working on the famous three-body problem when he discovered an interesting quirk in the results. Originally, he had set out to discover a way to easily calculate the gravitational interaction between arbitrary numbers of bodies in a system, because Newtonian mechanics conclude that such a system results in the bodies orbiting chaotically until there is a collision, or a body is thrown out of the system so that equilibrium can be achieved. The logic behind this conclusion is that a system with one body is trivial, as it is merely static relative to itself; a system with two bodies is very simple to solve for, as the bodies orbit around their common center of gravity. However, once more than two bodies are introduced, the mathematical calculations become very complicated. A situation arises where you would have to calculate every gravitational interaction between every pair of objects at every point along its trajectory. Lagrange, however, wanted to make this simpler. He did so with a simple hypothesis: The trajectory of an object is determined by finding a path that minimizes the action over time. This is found by subtracting the potential energy from the kinetic energy. With this way of thinking, Lagrange re-formulated the classical Newtonian mechanics to give rise to Lagrangian mechanics. With his new system of calculations, Lagrange’s work led him to hypothesize how a third body of negligible mass would orbit around two larger bodies which were already in a near-circular orbit. In a frame of reference that rotates with the larger bodies, he found five specific fixed points where the third body experiences zero net force as it follows the circular orbit of its host bodies (planets).[3] These points were named “Lagrangian points” in Lagrange's honor. It took over a hundred years before his mathematical theory was observed with the discovery of the Trojan asteroids in the 1900s at the Lagrange points of the Sun–Jupiter system. In the more general case of elliptical orbits, there are no longer stationary points in the same sense: it becomes more of a Lagrangian “area”. The Lagrangian points constructed at each point in time, as in the circular case, form stationary elliptical orbits which are similar to the orbits of the massive bodies. This is due to Newton's second law ( The Lagrangian points
A diagram showing the five Lagrangian points in a two-body system with one body far more massive than the other (e.g. the Sun and the Earth). In such a system, L3–L5 will appear to share the secondary's orbit, although in fact they are situated slightly outside it. The five Lagrangian points are labeled and defined as follows: L1 The L1 point lies on the line defined by the two large masses M1 and M2, and between them. It is the most intuitively understood of the Lagrangian points: the one where the gravitational attraction of M2 partially cancels M1 gravitational attraction. Example: An object which orbits the Sun more closely than the Earth would normally have a shorter orbital period than the Earth, but that ignores the effect of the Earth's own gravitational pull. If the object is directly between the Earth and the Sun, then the effect of the Earth's gravity is to weaken the force pulling the object towards the Sun, and therefore increase the orbital period of the object. The closer to Earth the object is, the greater this effect is. At the L1 point, the orbital period of the object becomes exactly equal to the Earth's orbital period. The Sun–Earth L1 is ideal for making observations of the Sun. Objects here are never shadowed by the Earth or the Moon. The Solar and Heliospheric Observatory (SOHO) is stationed in a Halo orbit at L1, and the Advanced Composition Explorer (ACE) is in a Lissajous orbit, also at the L1 point. The Earth–Moon L1 allows easy access to lunar and earth orbits with minimal change in velocity and would be ideal for a half-way manned space station intended to help transport cargo and personnel to the Moon and back. L2
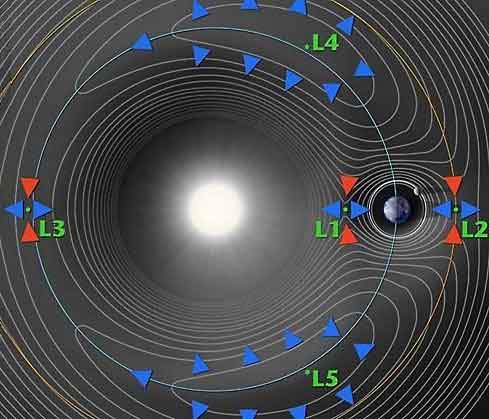
A diagram showing the Sun–Earth L2 point, which lies well beyond the Moon's orbit around the Earth. The L2 point lies on the line defined by the two large masses, beyond the smaller of the two. Here, the gravitational forces of the two large masses balance the centrifugal force on the smaller mass. Example: On the side of the Earth away from the Sun, the orbital period of an object would normally be greater than that of the Earth. The extra pull of the Earth's gravity decreases the orbital period of the object, and at the L2 point that orbital period becomes equal to the Earth's. The Sun–Earth L2 is a good spot for space-based observatories. Because an object around L2 will maintain the same orientation with respect to the Sun and Earth, shielding and calibration are much simpler. The Wilkinson Microwave Anisotropy Probe is already in orbit around the Sun–Earth L2. The future Herschel Space Observatory, Gaia probe, and James Webb Space Telescope will be placed at the Sun–Earth L2. Earth–Moon L2 would be a good location for a communications satellite covering the Moon's far side. If the mass of the smaller object (M2) is much smaller than the mass of the larger object (M1) then L1 and L2 are at approximately equal distances r from the smaller object, equal to the radius of the Hill sphere, given by: where R is the distance between the two bodies. This distance can be described as being such that the orbital period, corresponding to a circular orbit with this distance as radius around M2 in the absence of M1, is that of M2 around M1, divided by Examples: * Sun and Earth: 1,500,000 km from the Earth * Earth and Moon: 61,500 km from the Moon L3 The L3 point lies on the line defined by the two large masses, beyond the larger of the two. Example: L3 in the Sun–Earth system exists on the opposite side of the Sun, a little outside the Earth's orbit but slightly closer to the Sun than the Earth is.[4] Here, the combined pull of the Earth and Sun again causes the object to orbit with the same period as the Earth. The Sun–Earth L3 point was a popular place to put a "Counter-Earth" in pulp science fiction and comic books — though of course, once space based observation was possible via satellites and probes, it was shown to hold no such object. In actual fact, Sun–Earth L3 is highly unstable, because the gravitational forces of the other planets outweigh that of the Earth (Venus, for example, comes within 0.3 AU of L3 every 20 months). L4 and L5
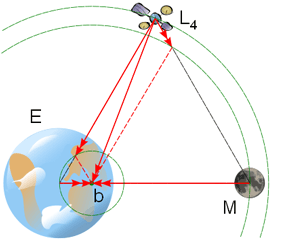
Gravitational accelerations at L4. The L4 and L5 points lie at the third corners of the two equilateral triangles in the plane of orbit whose common base is the line between the centres of the two masses, such that the point lies behind (L5) or ahead of (L4) the smaller mass with regard to its orbit around the larger mass. The reason these points are in balance is that, at L4 and L5, the distances to the two masses are equal. Accordingly, the gravitational forces from the two massive bodies are in the same ratio as the masses of the two bodies, and so the resultant force acts through the barycentre of the system; additionally, the geometry of the triangle ensures that the resultant acceleration is to the distance from the barycentre in the same ratio as for the two massive bodies. The barycentre being both the centre of mass and centre of rotation of the system, this resultant force is exactly that required to keep a body at the Lagrange point in orbital equilibrium with the rest of the system. (Indeed, the third body need not have negligible mass; the general triangular configuration was discovered by Lagrange in work on the 3-body problem.) L4 and L5 are sometimes called triangular Lagrange points or Trojan points. The name Trojan points comes from the Trojan asteroids at the Sun–Jupiter L4 and L5 points, which themselves are named after characters from Homer's Iliad (the legendary siege of Troy). Asteroids at the L4 point, which leads Jupiter, are referred to as the 'Greek camp', while at the L5 point they are referred to as the 'Trojan camp'. These asteroids are (largely) named after characters from the respective sides of the war. Examples: * The Sun–Earth L4 and L5 points lie 60° ahead of and 60° behind the Earth as it orbits the Sun. They contain interplanetary dust. * The Earth–Moon L4 and L5 points lie 60° ahead of and 60° behind the Moon as it orbits the Earth. They may contain interplanetary dust in what is called Kordylewski clouds. * The Sun–Jupiter L4 and L5 points are occupied by the Trojan asteroids. * Neptune has Trojan Kuiper Belt Objects at its L4 and L5 points. * Saturn's moon Tethys has two much smaller satellites at its L4 and L5 points named Telesto and Calypso, respectively. * Saturn's moon Dione has smaller moons Helene and Polydeuces at its L4 and L5 points, respectively. * The giant impact hypothesis suggests that an object named Theia formed at L4 or L5 and crashed into the Earth after its orbit destabilized, forming the moon. Stability The first three Lagrangian points are technically stable only in the plane perpendicular to the line between the two bodies. This can be seen most easily by considering the L1 point. A test mass displaced perpendicularly from the central line would feel a force pulling it back towards the equilibrium point. This is because the lateral components of the two masses' gravity would add to produce this force, whereas the components along the axis between them would balance out. However, if an object located at the L1 point drifted closer to one of the masses, the gravitational attraction it felt from that mass would be greater, and it would be pulled closer. (The pattern is very similar to that of tidal forces.) Although the L1, L2, and L3 points are nominally unstable, it turns out that it is possible to find stable periodic orbits around these points, at least in the restricted three-body problem. These perfectly periodic orbits, referred to as "halo" orbits, do not exist in a full n-body dynamical system such as the solar system. However, quasi-periodic (i.e. bounded but not precisely repeating) orbits following Lissajous curve trajectories do exist in the n-body system. These quasi-periodic Lissajous orbits are what all Lagrangian point missions to date have used. Although they are not perfectly stable, a relatively modest effort at station keeping can allow a spacecraft to stay in a desired Lissajous orbit for an extended period of time. It also turns out that, at least in the case of Sun–Earth L1 missions, it is actually preferable to place the spacecraft in a large amplitude (100,000–200,000 km) Lissajous orbit, instead of having it sit at the Lagrangian point, because this keeps the spacecraft off the direct Sun–Earth line, thereby reducing the impact of solar interference on the Earth–spacecraft communications links. Another interesting and useful property of the collinear Lagrangian points and their associated Lissajous orbits is that they serve as "gateways" to control the chaotic trajectories of the Interplanetary Transport Network. In contrast to the collinear Lagrangian points, the triangular points (L4 and L5) are stable equilibria (cf. attractor), provided that the ratio of M1/M2 is greater than 24.96[5][6]. This is the case for the Sun–Earth and, by a smaller margin, the Earth–Moon systems. When a body at these points is perturbed, it moves away from the point, but the Coriolis effect bends the object's path into a stable, kidney bean‐shaped orbit around the point (as seen in the rotating frame of reference). However, in the Earth–Moon case, the problem of stability is greatly complicated by the appreciable solar gravitational influence.[7] Intuitive explanation This section non-mathematically (intuitively[8]) explains the five Lagrangian points using the Earth–Moon system. Lagrangian points L2 through L5 only exist in rotating systems, as in the monthly orbiting of the Moon about the Earth. At these points, an outward (fictitious, as explained below) centrifugal force is balanced by the attractive gravitational forces of the Moon and Earth. Imagine using your hand to spin a stone at the end of a string. The string provides a tension force that continuously accelerates the stone towards the center. To an ant standing on the stone, however, it seems as if there is a force trying to fling him directly outward from the center. This apparent or fictitious force is called the centrifugal force . This same effect is present in the Earth–Moon system, where the role of the string is played by the summed (or net) effect of the two attractive gravities, and the stone is an asteroid or a spacecraft. The Earth–Moon system rotates about its combined center of mass, or barycenter. Because the Earth is much heavier than the Moon, this point is located within the Earth (about a thousand miles below the surface). Any object gravitationally held by the rotating Earth–Moon system will sense a centrifugal force directed away from the barycenter, in the same way as does the ant on our stone. Unlike the other Lagrangian points, L1 would exist even in a non-rotating (static or inertial) system. Rotation slightly pushes L1 away from the (heavier) Earth towards the (lighter) Moon. L1 is slightly unstable (see stability above) because drifting towards the Moon or Earth increases one gravitational attraction while decreasing the other, causing more drift. At Lagrangian points L2, L3, L4, and L5, a satellite feels an outward centrifugal force, away from the barycenter, that exactly balances the attractive gravity of the Earth and Moon. L2 and L3 are slightly unstable because small changes in satellite position more strongly affect gravity than the balancing centrifugal force. Stability at L4 and L5 depends crucially on the satellite being pulled in three different directions, namely the outward centrifugal force away from the barycenter, balancing the inward gravitational forces towards the Moon and Earth. Lagrangian point missions The Lagrangian point orbits have unique characteristics that have made them a good choice for performing some kinds of missions. NASA has operated a number of spacecraft in orbit around the Sun–Earth L1 and L2 points, including
ESA's Herschel Space Observatory (formerly called Far Infrared and Sub-millimetre Telescope or FIRST) in 2008 and the James Webb Space Telescope are also planned to be placed in orbit around L2.[9] ESA's Planck satellite planned for launch in 2008 will be placed in orbit around L2. The L5 Society was a precursor of the National Space Society, and promoted the possibility of establishing a colony and manufacturing facility in orbit around the L4 or L5 points in the Earth–Moon system (see Space colonization). The Earth–Moon L2 point has been proposed as a location for a communication satellite covering the far side of the Moon. NASA TN_D-4059 The Deep Space Climate Observatory was intended to be positioned at L1, but has been put into indefinite storage after being built. Natural examples In the Sun–Jupiter system several thousand asteroids, collectively referred to as Trojan asteroids, are in orbits around the Sun–Jupiter L4 and L5 points. Recent observations suggest that the Sun–Neptune L4 and L5 points, known as the Neptune Trojans, may be very thickly populated, containing large bodies an order of magnitude more numerous than the Jupiter Trojans. Other bodies can be found in the Sun–Mars and Saturn–Saturnian satellite systems. There are no known large bodies in the Sun–Earth system's Trojan points, but clouds of dust surrounding the L4 and L5 points were discovered in the 1950s. Clouds of dust, called Kordylewski clouds, even fainter than the notoriously weak gegenschein, may also be present in the L4 and L5 of the Earth–Moon system. The Saturnian moon Tethys has two smaller moons in its L4 and L5 points, Telesto and Calypso. The Saturnian moon Dione also has two Lagrangian co-orbitals, Helene at its L4 point and Polydeuces at L5. The moons wander azimuthally about the Lagrangian points, with Polydeuces describing the largest deviations, moving up to 32 degrees away from the Saturn–Dione L5 point. Tethys and Dione are hundreds of times more massive than their "escorts" (see the moons' articles for exact diameter figures; masses are not known in several cases), and Saturn is far more massive still, which makes the overall system stable. Other co-orbitals The Earth's companion object 3753 Cruithne is in a relationship with the Earth which is somewhat Trojan-like, but different from a true Trojan. This asteroid occupies one of two regular solar orbits, one of them slightly smaller and faster than the Earth's orbit, and the other slightly larger and slower. The asteroid periodically alternates between these two orbits due to close encounters with Earth. When the asteroid is in the smaller, faster orbit and approaches the Earth, it gains orbital energy from the Earth and moves up into the larger, slower orbit. It then falls farther and farther behind the Earth, and eventually Earth approaches it from the other direction. Then the asteroid gives up orbital energy to the Earth, and drops back into the smaller orbit, thus beginning the cycle anew. The cycle has no noticeable impact on the length of the year, because Earth's mass is over 20 billion (2 × 1010) times more than 3753 Cruithne. Epimetheus and Janus, satellites of Saturn, have a similar relationship, though they are of similar masses and so actually exchange orbits with each other periodically. (Janus is roughly 4 times more massive but still light enough for its orbit to be altered.) Another similar configuration is known as orbital resonance, in which orbiting bodies tend to have periods of a simple integer ratio, due to their interaction. Notes and references
See also * List of objects at Lagrangian points * Lunar space elevator * Home on Lagrange (The L5 Song) * L5 Society * Colonization of the Sun (Lagrange Points) * Horseshoe orbit Links
Retrieved from "http://en.wikipedia.org/"
|
|

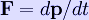 ), where p = mv (p the momentum, m the mass, and v the velocity) is invariant if force and position are scaled by the same factor. A body at a Lagrangian point orbits with the same period as the two massive bodies in the circular case, implying that it has the same ratio of gravitational force to radial distance as they do. This fact is independent of the circularity of the orbits, and it implies that the elliptical orbits traced by the Lagrangian points are solutions of the equation of motion of the third body.
), where p = mv (p the momentum, m the mass, and v the velocity) is invariant if force and position are scaled by the same factor. A body at a Lagrangian point orbits with the same period as the two massive bodies in the circular case, implying that it has the same ratio of gravitational force to radial distance as they do. This fact is independent of the circularity of the orbits, and it implies that the elliptical orbits traced by the Lagrangian points are solutions of the equation of motion of the third body.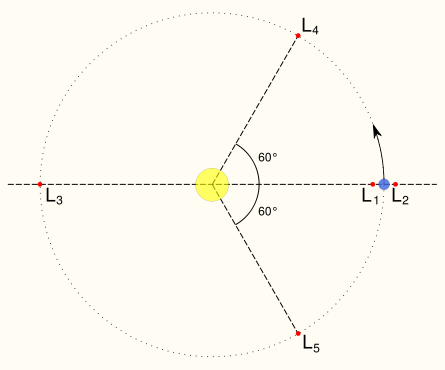

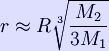
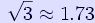 .
.