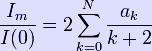Limb darkening refers to the diminishing of intensity in the image of a star as one moves from the center of the image to the edge or "limb" of the image. Limb darkening occurs as the result of two effects:

* The density of the star diminishes as the distance from the center increases

* The temperature of the star diminishes as the distance from the center increases.

Crucial to understanding limb darkening is the idea of optical depth. An optical depth of unity is that thickness of absorbing gas from which a fraction of 1/e photons can escape. This is what defines the visible edge of a star since it is at an optical depth of unity that the star becomes opaque. The radiation reaching us is closely approximated by the sum of all the emission along the entire line of sight, up to that point where the optical depth is unity. When we look near the edge of a star, we cannot "see" to the same depth as when we look at the center because the line of sight must travel at an oblique angle through the stellar gas when looking near the limb. In other words, the solar radius at which we see the optical depth as being unity increases as we move our line of sight towards the limb.

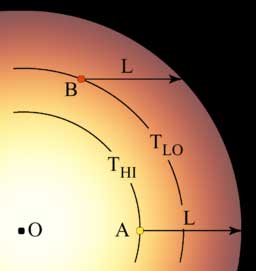
An idealized case of limb darkening. The outer boundary is the radius at which photons emitted from the star are no longer absorbed. L is a distance for which the optical depth is unity. High-temperature photons emitted at A will just barely escape from the star, as will the low temperature photons emitted at B.

The second effect is the fact that the effective temperature of the stellar atmosphere is (usually) decreasing for an increasing distance from the center of the star. The radiation emitted from a gas is a strongly increasing function of temperature. For a black body, for example, the spectrally integrated intensity is proportional to the fourth power of the temperature (Stefan-Boltzmann law). Since when we look at a star, at first approximation the radiation comes from the point at which the optical depth is unity, and that point is deeper in when looking at the center, the temperature will be higher, and the intensity will be greater, than when we look at the limb.

In fact, the temperature in the atmosphere of a star does not always decrease with increasing height, and for certain spectral lines, the optical depth is unity in a region of increasing temperature. In this case we see the phenomenon of "limb brightening". At very long (IR to radio) and very short (EUV to X-ray) wavelengths the situation becomes much more complicated. A coronal emission such as soft X-radiation will be optically thin and thus be characteristically limb-brightened. Further complication comes from the existence of rough (three-dimensional) structure. The classical analysis of stellar limb darkening, as described below, assumes the existence of a smooth hydrostatic equilibrium, and at some level of precision this assumption must fail (most obviously in sunspots and faculae, but generally everywhere). The analysis of these effects is presently in its infancy because of its computational difficulty [1].

Calculation of limb darkening

Limb darkening geometry. The star is centered at O and has radius R . The observer is at point P a distance r from the center of the star, and is looking at point S on the surface of the star. From the point of view of the observer, S is at an angle θ from a line through the center of the star, and the edge or limb of the star is at angle Ω.

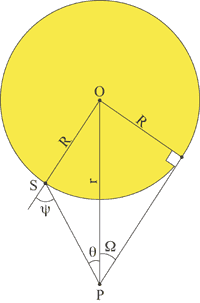
In the figure on the right, as long as the observer at point P is outside the stellar atmosphere, the intensity seen in the direction θ will be a function only of the angle of incidence ψ. This is most conveniently approximated as a polynomial in cos(ψ)

where I(ψ) is the intensity seen at P along a line of sight forming angle ψ with respect to the stellar radius, and I(0) is the central intensity. It can be seen that in order that the ratio be unity for ψ=0, we must have:

For example, for a Lambertian radiator (no limb darkening) we will have all a_k=0 except a₀=1. As another example, for the sun at 550 nm, the limb darkening is well expressed by N=2 and

(See Cox, 2000). Note - the equation for limb darkening is sometimes more conveniently written as:

which now has N independent coefficients rather than N+1 coefficients which must sum to unity.

We can convert from ψ to θ using the relationship:

}

where Ω is the angle from the observer to the limb of the star.

The above approximation can be used to derive an analytic expression for the ratio of the mean intensity to the central intensity. The mean intensity Im is the integral of the intensity over the disk of the star divided by the solid angle subtended by the disk:

where dω=sin(θ)dθdφ is a solid angle element and the integrals are over the disk: 0≤φ≤2π and 0≤θ≤Ω. Although this equation can be solved analytically, it is rather cumbersome. However, for an observer at infinite distance from the star, the above equation simplifies to:

References

* Billings, Donald E. (1966). A Guide to the Solar Corona. Academic Press, New York.

* Cox, Arthur N. (ed) (2000). Allen's Astrophysical Quantities, 14th ed., Springer-Verlag, NY. ISBN 0-387-98746-0.

* Milne, E.A. (1921). "". MNRAS 81: 361-375.

* Minnaert, M. (1930). "". Z.f. Ap. 1: 209.

* Neckel, H. and Labs, D. (1994). "Solar Limb Darkening 1986-1990". Solar Physics 153: 91-114. doi:10.1007/BF00712494.

* van de Hulst, H. C. (1950). "". Bull. Astron. Inst. Netherlands 11 (410): 135.

* Steiner, O., Photospheric processes and magnetic flux tubes, (2007) [1]

Retrieved from "http://en.wikipedia.org/"
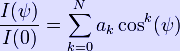
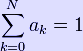
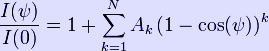
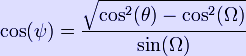All text is available under the terms of the GNU Free Documentation License