In quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation.[1][2] A classical (or non-quantum) algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a problem, where each step or instruction can be performed on a classical computer. Similarly, a quantum algorithm is a step-by-step procedure, where each of the steps can be performed on a quantum computer. Although all classical algorithms can also be performed on a quantum computer, the term quantum algorithm is usually used for those algorithms which seem inherently quantum, or use some essential feature of quantum computation such as quantum superposition or quantum entanglement. All problems which can be solved on a quantum computer can be solved on a classical computer. In particular, problems which are undecidable using classical computers remain undecidable using quantum computers. What makes quantum algorithms interesting is that they might be able to solve some problems faster than classical algorithms. The most well known algorithms are Shor's algorithm for factoring, and Grover's algorithm for searching an unstructured database or an unordered list. Shor's algorithms runs exponentially faster than the best known classical algorithm for factoring, the general number field sieve. Grover's algorithm runs quadratically faster than the best possible classical algorithm for the same task. Overview Quantum algorithms are usually described, in the commonly-used circuit model of quantum computation, by a quantum circuit which acts on some input qubits and terminates with a measurement. A quantum circuit consists of simple quantum gates which act on at most a fixed number of qubits, usually 2 or 3. Quantum algorithms may also be stated in other models of quantum computation, such as the Hamiltonian oracle model.[3] Quantum algorithms can be categorized by the main techniques used by the algorithm. Some commonly used techniques/ideas in quantum algorithms include phase kick-back, phase estimation, the quantum Fourier transform, quantum walks and amplitude amplification. Quantum algorithms may also be grouped by the type of problem solved, for instance see the survey on quantum algorithms for algebraic problems.[4] Algorithms based on the quantum Fourier transform The quantum Fourier transform is the quantum analogue of the discrete Fourier transform, and is used in several quantum algorithms. The Hadamard transform is also an example of a quantum Fourier transform. The quantum Fourier transform can be efficiently implemented on a quantum computer using only a polynomial number of quantum gates. Deutsch–Jozsa algorithm The Deutsch–Jozsa algorithm solves a black-box problem which provably requires exponentially many queries to the black box for any deterministic classical computer, but can be done with exactly 1 query by a quantum computer. If we allow both bounded-error quantum and classical algorithms, then there is no speedup since a classical probabilistic algorithm can solve the problem with a constant number of queries with small probability of error. Simon's algorithm Simon's algorithm solves a black-box problem exponentially faster than any classical algorithm, including bounded-error probabilistic algorithms. This algorithm, which achieves an exponential speedup over all classical algorithms that we consider efficient, was the motivation for Shor's factoring algorithm. Shor's algorithm Shor's algorithm solves the discrete logarithm problem and the integer factorization problem in polynomial time,[5] whereas the best known classical algorithms take super-polynomial time. These problems are not known to be in P or NP-complete. It is also one of the few quantum algorithms that solves a non–black-box problem in polynomial time where the best-known classical algorithms run in super-polynomial time. Hidden subgroup problem The abelian hidden subgroup problem is a generalization of many problems that can be solved by a quantum computer, such as Simon's problem, solving Pell's equation, testing the principal ideal of a ringR and factoring. There are efficient quantum algorithms known for the Abelian hidden subgroup problem.[6] The more general hidden subgroup problem, where the group isn't necessarily abelian, is a generalization of the previously-mentioned problems and graph isomorphism and certain lattice problems. Efficient quantum algorithms are known for certain non-abelian groups. However, no efficient algorithms are known for the symmetric group, which would give an efficient algorithm for graph isomorphism,[7] and the dihedral group, which would solve certain lattice problems.[8] Estimating Gauss sums A Gauss sum is a type of exponential sum. The best known classical algorithm for estimating these sums takes exponential time. Since the discrete logarithm problem reduces to Gauss sum estimation, an efficient classical algorithm for estimating Gauss sums would imply an efficient classical algorithm for computing discrete logarithms, which is considered unlikely. However, quantum computers can estimate Gauss sums to polynomial precision in polynomial time.[9] Algorithms based on amplitude amplification Amplitude amplification is a technique that allows the amplification of a chosen subspace of a quantum state. Applications of amplitude amplification usually lead to quadratic speedups over the corresponding classical algorithms. It can be considered to be a generalization of Grover's algorithm. Grover's algorithm Grover's algorithm searches an unstructured database (or an unordered list) with N entries, for a marked entry, using only Quantum counting Quantum counting solves a generalization of the search problem. It solves the problem of counting the number of marked entries in an unordered list, instead of just detecting if one exists. Specifically, it counts the number of marked entries in an N-element list, with error ε making only Algorithms based on quantum walks A quantum walk is the quantum analogue of a classical random walk. Similar to a classical random walk, which can be described by a probability distribution over some states, a quantum walk can be described by a quantum superposition over states. Quantum walks are known to give exponential speedups for some black-box problems.[13][14] They also provide polynomial speedups for many problems. Element distinctness problem The element distinctness problem is the problem of determining whether all the elements of a list are distinct. Classically, Ω(N) queries are required for a list of size N, since this problem is harder than the search problem which requires Ω(N) queries. However, it can be solved in Θ(N2 / 3) queries on a quantum computer. The optimal algorithm is by Andris Ambainis,[15] and the lower bound is due to Scott Aaronson and Yaoyun Shi.[16] Triangle-finding problem The triangle-finding problem is the problem of determining whether a given graph contains a triangle (a clique of size 3). The best-known lower bound for quantum algorithms is Ω(N), but the best algorithm known requires O(N1.3) queries.[17] Evaluating NAND trees The problem is to compute the value of a formula given by a balanced binary tree with bits at the leaves, and NAND gates at the inner vertices.[18] This problem requires Θ(N0.753) queries classically, but can be solved in Θ(N0.5) queries by a quantum algorithm.[19] Quantum Simulation The idea that quantum computers might be more powerful than classical computers originated in Richard Feynman's observation that classical computers seem to require exponential time to simulate many-particle quantum systems.[20] Since then, the idea that quantum computers can simulate quantum physical processes exponentially faster than classical computers has been greatly fleshed out and elaborated. Efficient (that is, polynomial-time) quantum algorithms have been developed for simulating both Bosonic and Fermionic systems[21] and in particular, the simulation chemical reactions beyond the capabilities of current classical supercomputers requires only a few hundred qubits.[22] Quantum computers can also efficiently simulate topological quantum field theories.[23] In addition to its intrinsic interest, this result has let to efficient quantum algorithms for estimating "quantum" topological invariants such as Jones[24] and HOMFLY[25] polynomials, and the Turaev-Viro invariant of three-dimensional manifolds.[26] References 1. ^ Michael Nielsen and Isaac Chuang (2000). Quantum Computation and Quantum Information. Cambridge: Cambridge University Press. ISBN 0-521-63503-9. OCLC 174527496.
* The Quantum Algorithm Zoo: A comprehensive list of quantum algorithms that provide a speedup over the fastest known classical algorithms.
Retrieved from "http://en.wikipedia.org/"
 |
|
||||||||||||
queries instead of the Ω(N) queries required classically.[10] Classically, Ω(N) queries are required, even if we allow bounded-error probabilistic algorithms.
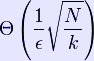queries, where k is the number of marked elements in the list.[11][12]