.
Mikhail Vasilievich Ostrogradsky

Mikhail Vasilievich Ostrogradsky or Mykhailo Vasyliovych Ostrohradsky (transcribed also Ostrohradskyy, Ostrogradskii, Ostrogradskiĭ) (Russian: Михаил Васильевич Остроградский, Ukrainian: Михайло Васильович Остроградський September 24, 1801 - January 1, 1862) was a Russian mathematician, mechanician and physicist. Ostrogradsky is considered to be a disciple of Leonhard Euler and one of the leading mathematicians of Imperial Russia.
Ostrogradsky was born in Pashennaya (Пашенная), Ukraine, Russian Empire. From 1816 to 1820 he studied under Timofei Fedorovich Osipovsky (1765-1832) and graduated from the University of Kharkiv. When 1820 Osipovsky was suspended on religious grounds, Ostrogradsky refused to be examined and he never received his Doctor's degree. From 1822 to 1826 he studied at the Sorbonne and at the Collège de France in Paris, France. In 1828 he returned to the Russian Empire and settled in Saint Petersburg, where he was elected a member of the Academy of Sciences.
He worked mainly in the mathematical fields of calculus of variations, integration of algebraic functions, number theory, algebra, geometry, probability theory and in the fields of mathematical physics and classical mechanics. In the latter his most important work includes researches of the motion of an elastic body and the development of methods for integration of the equations of dynamics. Here he continued works of Euler, Joseph Louis Lagrange, Siméon-Denis Poisson and Augustin Louis Cauchy. His work in these fields was in Russia continued by Nikolay Dmitrievich Brashman (1796-1866), August Yulevich Davidov (1823-1885) and specially by the brilliant work of Nikolai Yegorovich Zhukovsky (1847-1921).
Ostrogradsky did not appreciate the work on non-euclidean geometry of Nikolay Ivanovich Lobachevsky from 1823 and he rejected it, when it was submitted for publication in the Saint Petersburg Academy of Sciences.
His method for integrating the rational functions is well known. With his equation we separate integral of a fractional rational function, the sum of the rational part (algebraic fraction) and the transcendental part (with the logarithm and the arctangent). We determine the rational part without integrating it and we assign a given integral into Ostrogradsky's form:
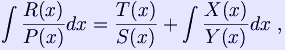
where P(x), S(x), Y(x) are known polynomials of degrees p, s and y, R(x) known polynomial of degree not greater than p-1, T(x) and X(x) unknown polynomials of degrees not greater than s-1 and y-1 respectively.
Ostrogradsky died in Poltava (Полтава), Ukraine, Russian Empire.
See also:
Divergence theorem (Ostrogradsky-Gauss theorem / Gauss-Ostrogradsky // Green-Ostrogradsky-Gauss / Gauss-Green-Ostrogradsky)
Ostrogradsky's equation
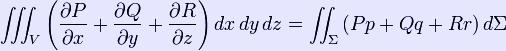 Green's theorem (1827)
Green's theorem (1827)
Green-Ostrogradsky equation (1828)
Hamilton-Ostrogradsky (variational) principle
Ostrogradsky formalism
Einstein-Ostrogradsky-Dirac Hamiltonian
Horowitz-Ostrogradsky method
Jacobi-Ostrogradsky coordinates
External links
* O'Connor, John J.; Robertson, Edmund F., "Mikhail Vasilievich Ostrogradsky", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Ostrogradski.html .
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License


