Omega constant

The Omega constant is a mathematical constant defined by

It is the value of W(1) where W is Lambert's W function. The name is derived from the alternate name for Lambert's W function, the Omega function.

The value of Ω is approximately 0.5671432904097838729999686622 (sequence A030178 in OEIS). It has properties that

or equivalently,

One can calculate Ω iteratively, by starting with an initial guess Ω0, and considering the sequence

This sequence will converge towards Ω as n→∞.

Irrationality and transcendence

Ω can be proven irrational from the fact that e is transcendental; if Ω were rational, then there would exist integers p and q such that

so that

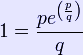
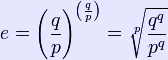
and e would therefore be algebraic of degree p. However e is transcendental, so Ω must be irrational.

Ω is in fact transcendental as the direct consequence of Lindemann–Weierstrass theorem. If Ω were algebraic, exp(Ω) would be transcendental and so would be exp−1(Ω). But this contradicts the assumption that it was algebraic.