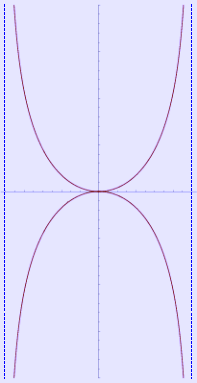
The kappa curve has two vertical asymptotes.
Kappa curve
In geometry, the kappa curve or Gutschoven's curve is a two-dimensional algebraic curve resembling the Greek letter κ (kappa).
Using the Cartesian coordinate system it can be expressed as:
x4 + x2y2 = a2y2
or, using parametric equations:
![]()
In polar coordinates its equation is even simpler:
r = atanθ
It has two vertical asymptotes at x=\pm a, they have been denoted as blue dashed lines on the graphic.
The kappa curve's curvature:
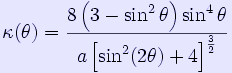 }
}
Tangential angle:
![]()
The kappa curve was first studied by Gérard van Gutschoven around 1662. Other famous mathematicians who have studied it include Isaac Newton and Johann Bernoulli. Its tangents were first calculated by Isaac Barrow in the 17th century.
Links
* Eric W. Weisstein, Kappa curve at MathWorld.
* A Java applet for playing with the curve
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

