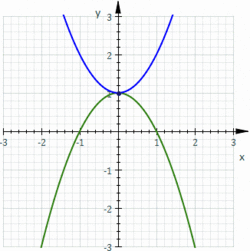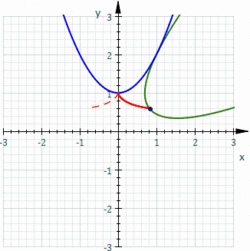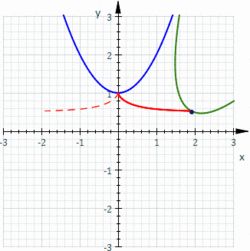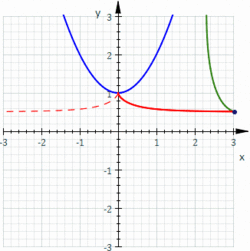
Construction of a roulette, in fact a cissoid of Diocles.
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, and involutes. Take two curves. Fix some point, called the generator or pole, in relation to the first curve. Roll the first curve along the second; the generator traces out a curve. Such a curve is called a roulette.
More precisely, the curves must be differentiable curves in the Euclidean plane. One is kept invariant; the other is subjected to a continuous congruence transformation such that at all times the curves are tangent at a point of contact that moves with the same speed when taken along either curve. The resulting roulette is formed by the locus of the generator subjected to the same set of congruence transformations.
Modelling the original curves as curves in the complex plane, let ![]() be differentiable parametrisations such that t r(0) = f(0), r'(0) = f'(0), and
be differentiable parametrisations such that t r(0) = f(0), r'(0) = f'(0), and ![]() for all t. ,. The roulette of
for all t. ,. The roulette of ![]() as r is rolled on f is then given by the mapping:
as r is rolled on f is then given by the mapping:
![]() .
.
Roulettes in higher spaces can certainly be imagined but one needs to align more than just the tangents.
A Sturm roulette traces the center of a conic section as the section rolls on a line.[1] A Delaunay roulette traces a focus of a conic section as the section rolls on a line.[2]
Example
If the fixed curve is a catenary and the rolling curve is a line, we have:
![]()
f'(t)=1+i\sinh(t) \qquad r'(t)=\cosh(t).
![]()
The parameterization of the line is chosen so that
![]()
![]()
![]()
![]()
Applying the formula above we obtain:
![]() }.
}.
If p = −i the expression is real and the roulette is a horizontal line. In other words, a square wheel could roll without bouncing in a road that was a matched series of catenary arcs.
Links
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

