.
Bifurcation diagram
In mathematics, particularly in dynamical systems, a bifurcation diagram shows the possible long-term values (equilibria/fixed points or periodic orbits) of a system as a function of a bifurcation parameter in the system. It is usual to represent stable solutions with a solid line and unstable solutions with a dotted line.
Bifurcations in the Logistic Map
An example is the bifurcation diagram of the logistic map:
![]()
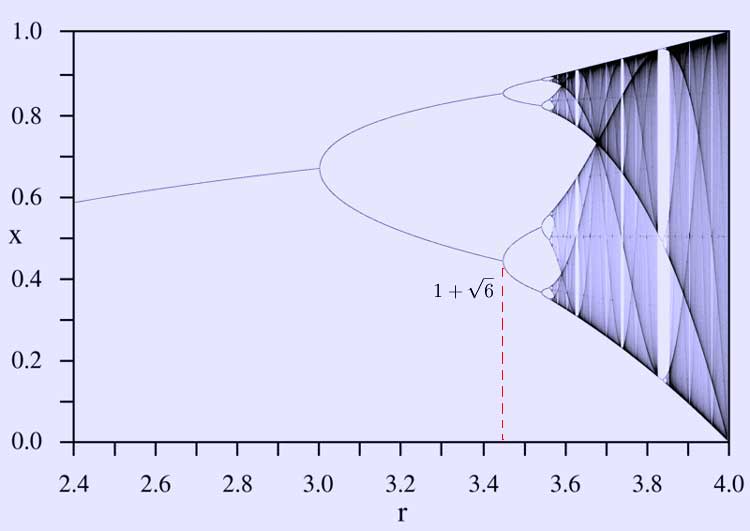
The bifurcation parameter r is shown on the horizontal axis of the plot and the vertical axis shows the possible long-term population values of the logistic function. Only the stable solutions are shown here, there are many other unstable solutions which are not shown in this diagram.
The bifurcation diagram nicely shows the forking of the possible periods of stable orbits from 1 to 2 to 4 to 8 etc. Each of these bifurcation points is a period-doubling bifurcation. The ratio of the lengths of successive intervals between values of r for which bifurcation occurs converges to the first Feigenbaum constant.
Bifurcation Diagram with Mathematica
Logistic Map
map[r_] := r#(1 - #) &;
Orbit
orbit[r_, x0_, n_] := NestList[r#(1 - #) &, x0, n];
Plot of the orbit
plotorbit[r_, start_, n_, Opts___] :=
ListPlot[NestList[r#(1 - #) &, start, n],
Opts,
PlotStyle -> {AbsolutePointSize[4], RGBColor[1, 0, 0]},
GridLines -> Automatic,
Epilog ->
ListPlot[NestList[r#(1 - #) &, start, n],
PlotJoined -> True,
DisplayFunction -> Identity
][[1]]
]
Plot of orbit for r = 2.8, 100 steps
plotorbit[2.8, 0.1, 100, AxesLabel -> {n, x\_i}];
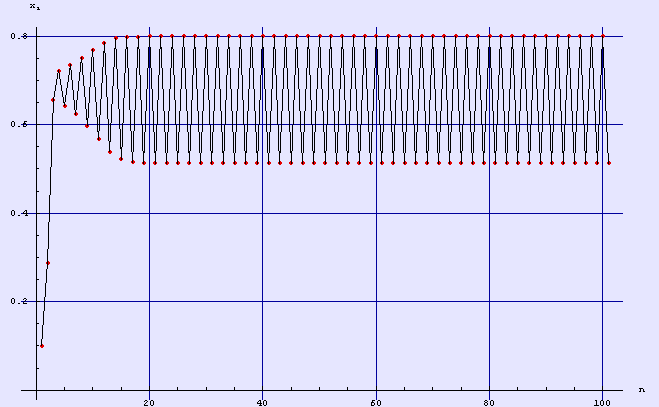
Take from the 500 points only the last 100:
Lval = Compile[{α}, ({α, #} &) /@ Drop[NestList[α#(1 - #) &, 0.5, 500], 400]];
bifurcation[α0_, α1_, n_] := Flatten[Table[Lval[α], {α, α0, α1, (α1 - α0)/ n}], 1];
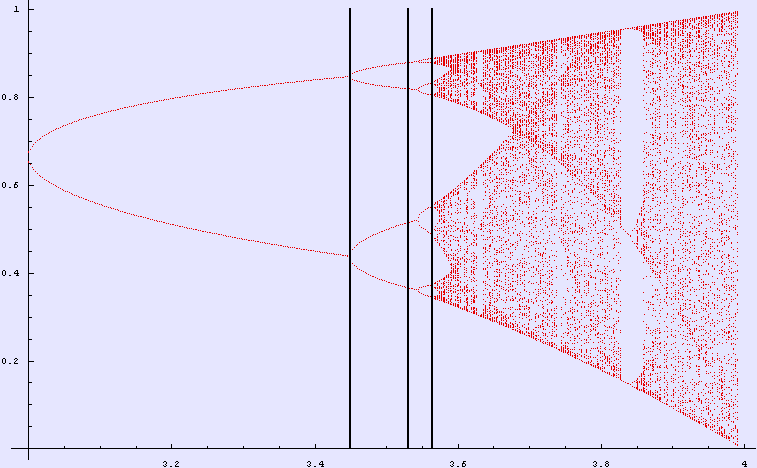
Calculate the diagram from r = 3 to r = 3.99 in 400 steps
Spoints = bifurcation[3, 3.99, 400];
pt1 = ListPlot[Spoints, PlotStyle -> {RGBColor[1, 0, 0], AbsolutePointSize[1.5]}, Epilog -> {Thickness[0.004],
Line[{{#, 0}, {#, 1}}] & /@ {3.45, 3.53, 3.564}}];
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

