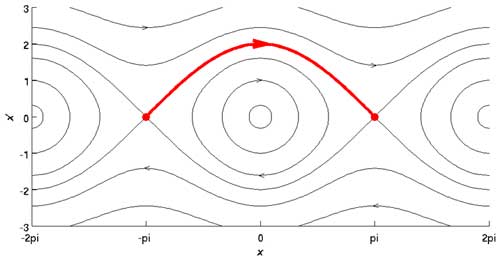
In mathematics, in the phase portrait of a dynamical system, a heteroclinic orbit (sometimes called a heteroclinic connection) is a path in phase space which joins two different equilibrium points. If the equilibrium points at the start and end of the orbit are the same, the orbit is a homoclinic orbit.

The phase portrait of the pendulum equation x'' + sin x = 0. The highlighted curve shows the heteroclinc orbit from (x, x') = (−π, 0) to (x, x') = (π, 0). This orbit corresponds with the (rigid) pendulum starting upright, making one revolution through its lowest position, and ending upright again.

Consider the continuous dynamical system described by the ODE

Suppose there are equilibria at x = x0 and x = x1, then a solution φ(t) is a heteroclinic orbit from x0 to x1 if

and

This implies that the orbit is contained in the stable manifold of x1 and the unstable manifold of x0.

See also

* Heteroclinic cycle
* Heteroclinic bifurcation
* Homoclinic orbit

References

* John Guckenheimer and Philip Holmes, Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, (Applied Mathematical Sciences Vol. 42), Springer

Dynamical System