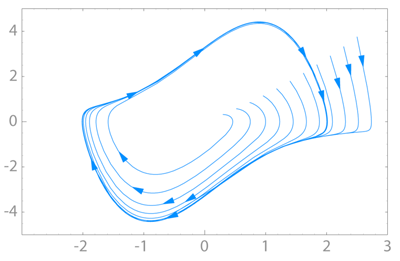
In mathematics, in the area of dynamical systems, a limit-cycle on a plane or a two-dimensional manifold is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches minus-infinity. Such behavior is exhibited in some nonlinear systems. In the case where all the neighboring trajectories approach the limit-cycle as time Stable limit-cycles imply self sustained oscillations. Any small perturbation from the closed trajectory would cause the system to return to the limit-cycle, making the system stick to the limit-cycle.
(*) Figure illustrating a stable limit cycle for the Van der Pol oscillator. As seen in the figure, trajectories for various initial states of this system converge to the limit cycle. Hence, this system exhibits self-sustained oscillations. The number of limit cycles of a polynomial differential equation is the main object of the second part of Hilbert's sixteenth problem. Bendixson's theorem and the Poincaré-Bendixson theorem predict the absence or existence, respectively, of limit cycles of two-dimensional nonlinear dynamical systems. Limit cycles can appear in quantized systems such as sigma-delta DAC. They appear as faint tones when trying to reconstruct a constant amplitude. Modern DACs have various mechanisms to detect and cancel such tones. See also * Periodic point * Stable manifold * Hyperbolic set References * limit cycle on PlanetMath * Steven H. Strogatz, "Nonlinear Dynamics and Chaos", Addison Wesley publishing company, 1994. * M. Vidyasagar, "Nonlinear Systems Analysis, second edition, Prentice Hall, Englewood Cliffs, New Jersey 07632. * Philip Hartman, "Ordinary Differential Equation", Society for Industrial and Applied Mathematics, 2002. * Witold Hurewicz, "Lectures on Ordinary Differential Equations", Dover, 2002. * Solomon Lefschetz, "Differential Equations: Geometric Theory", Dover, 2005. * Lawrence Perko, "Differential Equations and Dynamical Systems", Springer-Verlag, 2006. Retrieved from "http://en.wikipedia.org/"
|
|
, it is called a stable or attractive limit-cycle. If instead all neighboring trajectories approach it as time
, it is an unstable or non-attractive limit-cycle. In all other cases it is neither "stable" nor "unstable".
