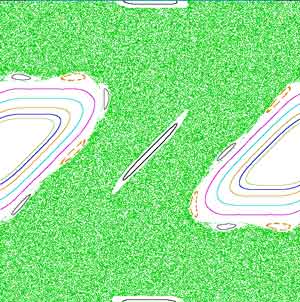
Example of the mapping of ten orbits of the Standard map for K = 2.0. The large green region is the main chaotic region of the map. (*) The Standard map (also known as Chirikov-Taylor map or Chirikov standard map[1]) is an area-preserving chaotic map from a square with side 2π onto itself. It is defined by: pn + 1 = pn + Ksin(θn) θn + 1 = θn + pn + 1 where pn and θn are taken modulo 2π. This map describes the motion of a simple mechanical system called a kicked rotator. This is made by a stick that is free of the gravitational force, which can rotate frictionless in a plane around an axis located in one of its tips, and which is periodically kicked on the other tip. The variables θn and pn respectively determine the angular position of the stick and its angular momentum after the n-th kick. The constant K measures the intensity of the kicks. Besides the kicked rotator, the standard map also describes other systems in the fields of mechanics of particles, accelerator physics, plasma physics, and solid state physics. However, this map is interesting from a fundamental point of view in physics and mathematics because it is a very simple model of a conservative system that displays hamiltonian chaos. It is therefore useful to study the development of chaos in this kind of system. For K = 0 the map is linear and only periodic and quasiperiodic orbits are allowed. When plotted in phase space (the θ–p plane), periodic orbits appear as closed curves, and quasiperiodic orbits as necklaces of closed curves whose centers lie in another larger closed curve. Which type of orbit is observed depends on the map's initial conditions. Nonlinearity of the map increases with K, and with it the possibility to observe chaotic dynamics for appropriate initial conditions. This is illustrated in the figure, which displays a collection of different orbits allowed to the standard map for a value of K > 0. Each orbit starts from a different initial condition, and different colors are used to distinguish the distinct orbits. All the orbits shown are periodic or quasiperiodic, with the exception of the green one that is chaotic and develops in a large region of phase space as an apparently random set of points. History The properties of chaos of the standard map were established by Boris Chirikov in 1969. See more details at Chirikov standard map. Books * Lichtenberg, A.J. and Lieberman, M.A. (1992). Regular and Chaotic Dynamics. Springer, Berlin. ISBN 978-0-387-97745-4. Springer link * Ott, Edward (2002). Chaos in Dynamical Systems. Cambridge University Press New, York. ISBN 0-521-01084-5. * Sprott, Julien Clinton (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN 0-19-850840-9. Links * Chirikov standard map at Scholarpedia * Website dedicated to Boris Chirikov * Interactive Java Applet visualizing orbits of the Standard Map, by Achim Luhn Retrieved from "http://en.wikipedia.org/"
|
|