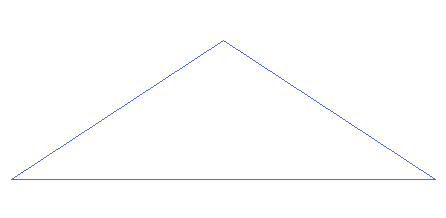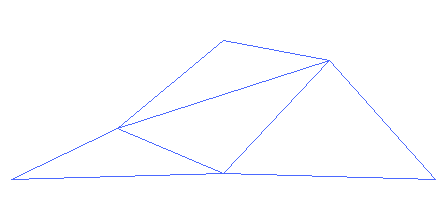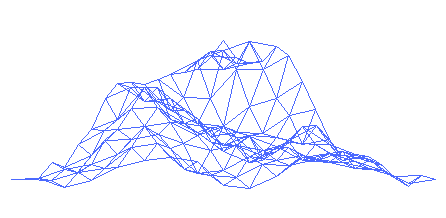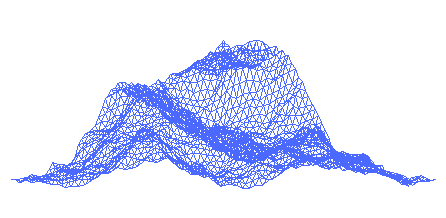
A fractal landscape is essentially a two-dimensional form of the fractal coastline, which can be considered a stochastic generalization of the Koch curve. The Hausdorff-Besicovitch dimension, D, is a fraction between 2 and 3. A way to make such a landscape is to employ the random midpoint displacement algorithm, in which a square is subdivided into four smaller equal squares and the center point is vertically offset by some random amount. The process is repeated on the four new squares, and so on, until the desired level of detail is reached. There are many fractal procedures (such as Perlin noise) capable of creating terrain data, however, the term "fractal landscape" has become more generic. F. Kenton "Doc Mojo" Musgrave is considered a leading authority on fractal landscapes. His computer program, MojoWorld,[1] is one of the more convenient ways to investigate them. The core of Dr. Musgrave's work in this area centered on rendering planetary bodies from orbital heights smoothly down to the surface with adaptive level of detail. Mojoworld basically makes this process interactive for anyone with a sufficiently powerful PC. Another program in this vein is Matt Fairclough's Terragen.[2] Terragen, landscape generator. See also References 2. ^ Terragen Links * Pandromeda's MojoWorld Generator * 3D Fractal Mountains in Java * MDTerrain Terrain Generator using Midpoint Displacement * Landscape Studio Java-based terrain generator * A Web-Wide World by Ken Perlin, 1998; a Java applet showing a sphere with a generated landscape.
Retrieved from "http://en.wikipedia.org/" |
|