.
Cantitruncated 600-cell
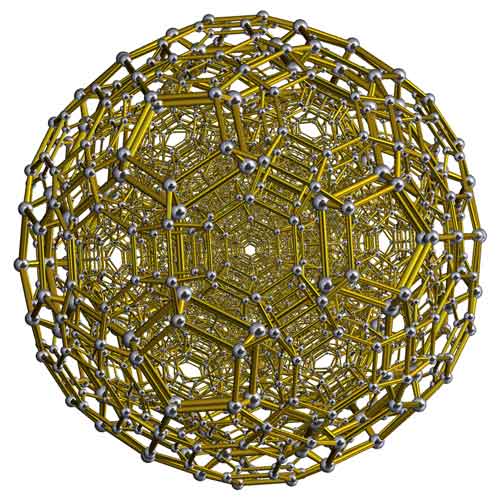
Cantitruncated 600-cell (*)
In geometry, the cantitruncated 600-cell is a uniform polychoron.
References
* Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
o (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
o (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
o (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
* J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
* N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
* Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation [2]
External links
* Convex uniform polychora based on the hecatonicosachoron (120-cell) and hexacosichoron (600-cell) - Model 45, George Olshevsky.
* Archimedisches Polychor Nr. 61 (cantitruncated 600-cell) Marco Möller's Archimedean polytopes in R4 (German)
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

