.
Cyclic quadrilateral
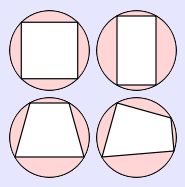
Cyclic quadrilaterals.
In geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. The vertices are said to be concyclic.
In a cyclic quadrilateral, opposite angles are supplementary (their sum is π radians). Equivalently, each exterior angle is equal to the opposite interior angle.
The area of a cyclic quadrilateral is given by Brahmagupta's formula as long as the sides are given. This area is maximal among all quadrilaterals having the same side lengths.
Ptolemy's theorem expresses the product of the lengths of the two diagonals of a cyclic quadrilateral as equal to the sum of the products of opposite sides. In any convex quadrilateral, the two diagonals together partition the quadrilateral into four triangles; in a cyclic quadrilateral, opposite pairs of these four triangles are similar to each other.
Any square, rectangle, or isosceles trapezoid is cyclic.
See also
* Cyclic polygon
Links
* Book 3, Proposition 22 of Euclid's Elements
* Cyclic quadrilateral theorem by Antonio Gutierrez from "Geometry Step by Step from the Land of the Incas".
* Incenters in Cyclic Quadrilateral at cut-the-knot
* Four Concurrent Lines in a Cyclic Quadrilateral at cut-the-knot
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

