.
Disphenoid
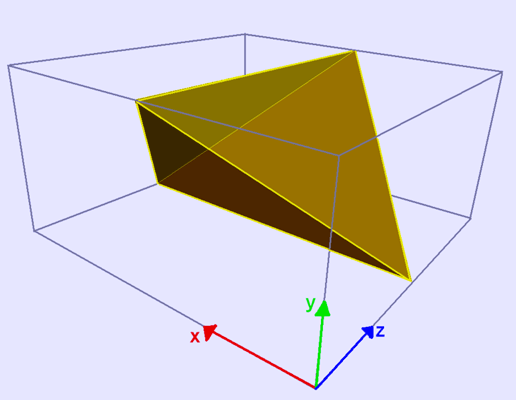
Disphenoid tetrahedron inside a square cuboid
A disphenoid is a polyhedron whose four faces are identical isosceles or scalene triangles.[1] (A regular tetrahedron has four identical triangular faces, but is not normally considered a disphenoid.) The faces of a tetragonal disphenoid are isosceles; the faces of a rhombic disphenoid are scalene.
All the solid angles and vertex figures of a disphenoid are the same. However, a disphenoid is not a regular polyhedron, because its faces are not regular polygons.
Some tetragonal disphenoids will form honeycombs. The disphenoid whose four vertices are (-1, 0, 0), (1, 0, 0), (0, 1, 1), and (0, 1, -1) is a such a disphenoid.[2] Each of its four faces is an isosceles triangle with edges of lengths √3, √3, and 2. It can tesselate space to form the disphenoid tetrahedral honeycomb. As Gibb[3] describes, it can be folded without cutting or overlaps from a single sheet of a4 paper.
References
1. ^ *Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. p. 15
2. ^ Coxeter, pp. 71–72; Senechal, Marjorie (1981). "Which tetrahedra fill space?". Mathematics Magazine 54 (5): 227–243.
3. ^ Gibb, William (1990). "Paper patterns: solid shapes from metric paper". Mathematics in School 19 (3): 2–4. Reprinted in Pritchard, Chris, ed. (2003). The Changing Shape of Geometry: Celebrating a Century of Geometry and Geometry Teaching. Cambridge University Press, 363–366. ISBN 0-521-53162-4.
# OBJ
# Disphenoid tetrahedron
v -1 0 0
v 1 0 0
v 0 1 1
v 0 1 -1
f 1 2 3
f 1 2 4
f 1 3 4
f 2 3 4
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

