.
E6 polytope
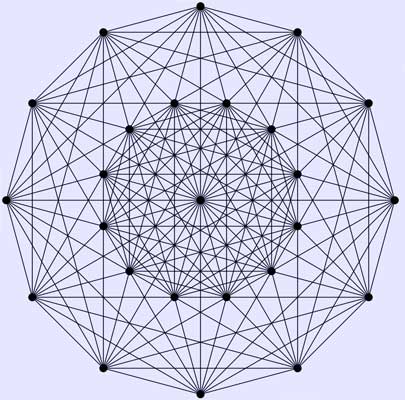
E6 polytope, Vertex-edge graph (*)
| E6 polytope | |
|---|---|
| Type | Uniform 6-polytope |
| Family | Semiregular E-polytope |
| Schläfli symbol | t0{32,2,1} |
| Coxeter-Dynkin diagram |
|
| 5-faces | 99 total: 27 pentacrosses and 72 5-simplices |
| 4-faces | 648 pentachorons |
| Cells | 1080 tetrahedrons |
| Faces | 720 triangles |
| Edges | 216 |
| Vertices | 27 |
| Vertex figure | demipenteract: {31,2,1} |
| Symmetry group | E6, [32,2,1] |
| Properties | convex |
The E6 polytope is a semiregular polytope, discovered by Thorold Gosset, published in his 1900 paper. He called it an 6-ic semi-regular figure
Its construction is based on the E6 group. It is also named by Coxeter as 221 by its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of one of the 2-node sequence.
It is also one of a family of 39 convex uniform polytopes in 6-dimensions, made of uniform polytope facets and vertex figures, defined by all permutations of ringed Coxeter-Dynkin diagrams.
See also
* 6-polytope
* Semiregular E-polytope
References
* T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
* A. Boole Stott: Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
* Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
o (Paper 17) Coxeter, The Evolution of Coxeter-Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233-248] See figure 1: (p.232) (Node-edge graph of polytope)
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

