.
Japanese theorem for cyclic polygons
In geometry, the Japanese theorem states that no matter how one triangulates a cyclic polygon, the sum of inradii of triangles is constant.
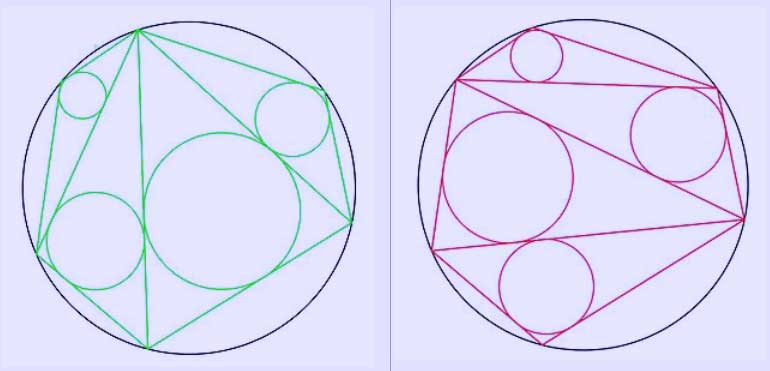
sum of the radii of the green circles = sum of the radii of the red circles
Conversely, if the sum of inradii independent from the triangulation, then the polygon is cyclic. The Japanese theorem follows from the Carnot's theorem; it is a Sangaku problem.
This theorem also follows from a simple extension of the Japanese theorem for cyclic quadrilaterals. That theorem shows that a rectangle is formed by the two pairs of incenters corresponding to the two possible triangulations of the quadrilateral. The steps of this theorem require nothing beyond basic constructive Euclidean geometry.
With the additional construction of a parallelogram having sides parallel to the diagonals, and tangent to the corners of the rectangle of incenters, the quadrilateral case of the concyclic polygon theorem can be proved in a few steps. The equality of the sums of the radii of the two pairs is equivalent to the condition that the constructed parallelogram be a rhombus, and this is easily shown in the construction.
Also, it's readily shown that the quadrilateral case suffices to prove the general case of the concyclic polygon theorem. The quadrilateral rule can be applied to quadrilateral components of a general partition of a cyclic polygon, and repeated application of the rule, which "flips" one diagonal, will generate all the possible partitions from any given partition, with each "flip" preserving the sum of the inradii. Hence the concyclic polygon theorem considered here can be regarded as a corollary of the extended cyclic quadrilateral theorem.
See also
Carnot's theorem, which is used in a proof of the theorem above
Equal incircles theorem
Tangent lines to circles
External links
Japanese theorem in Mathworld
Japanese Theorem interactive demonstration at the C.a.R. website
More on Sangaku and this theorem from Mathtrek
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

