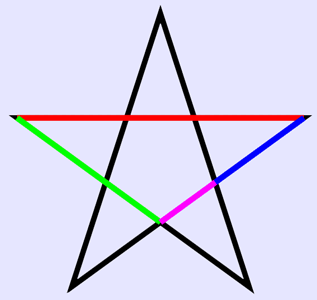
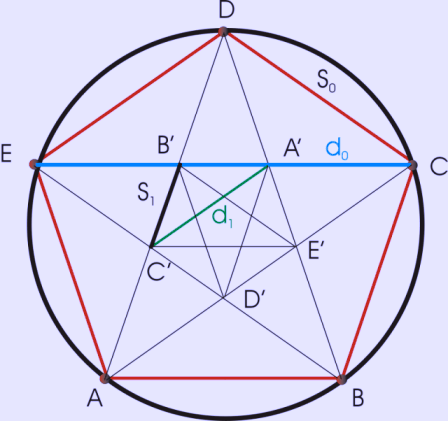
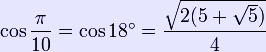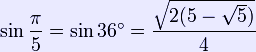A pentagram (sometimes known as a pentalpha or pentangle or, more formally, as a star pentagon) is the shape of a five-pointed star drawn with five straight strokes. The word pentagram comes from the Greek word πεντάγραμμον (pentagrammon), a noun form of πεντάγραμμος (pentagrammos) or πεντέγραμμος (pentegrammos), a word meaning roughly "five-lined" or "five lines".

Pentagrams were used symbolically in ancient Greece and Babylonia.

Early history

Sumer

The first known uses of the pentagram are found in Mesopotamian writings dating to about 3000 BC. The Sumerian pentagrams served as pictograms for the word "UB," meaning "corner, angle, nook; a small room, cavity, hole; pitfall," suggesting something very similar to the pentemychos (see below on the Pythagorean use for what pentemychos means). In René Labat's index system of Sumerian hieroglyphs/pictograms it is shown with two points up.[6]

Pythagoreans

The Pythagoreans called the pentagram ύγιεια Hygieia ("health"; also the Greek goddess of health, Hygieia), and saw in the pentagram a mathematical perfection (see Geometry section below).

The five vertices were also used by the medieval neo-pythagoreans (whom one could argue were not pythagoreans at all) to represent the five classical elements:

* ύδωρ, Hydor, water

* Γαια, Gaia earth

* ίδέα, Idea or ίερόν, Hieron "a divine thing"

* έιλή, Heile, heat (fire)

* άήρ, Aer, air

The vertices were labeled in the letters of υ-γ-ι-ει-α. The ordering (clockwise or counter-clockwise) and starting vertex varied.

The ancient Pythagorean pentagram was drawn with two points up and represented the doctrine of Pentemychos. Pentemychos means "five recesses" or "five chambers", also known as the pentagonas — the five-angle, and was the title of a work written by Pythagoras's teacher and friend Pherecydes of Syros.[7]

Geometry

The pentagram is the simplest regular star polygon. The pentagram contains ten points (the five points of the star, and the five vertices of the inner pentagon) and fifteen line segments. It is represented by the Schläfli symbol {5/2}. Like a regular pentagon, and a regular pentagon with a pentagram constructed inside it, the regular pentagram has as its symmetry group the dihedral group of order 10.

Construction

The pentagram can be constructed by connecting alternate vertices of a pentagon; see details of the construction. It can also be constructed as a stellation of a pentagon, by extending the edges of a pentagon until the lines intersect.

Golden ratio

The golden ratio, φ = (1+√5)/2 ≈ 1.618, satisfying

plays an important role in regular pentagons and pentagrams. Each intersection of edges sections the edges in golden ratio: the ratio of the length of the edge to the longer segment is φ, as is the length of the longer segment to the shorter. Also, the ratio of the length of the shorter segment to the segment bounded by the 2 intersecting edges (a side of the pentagon in the pentagram's center) is φ. As the four-color illustration shows:

The pentagram includes ten isosceles triangles: five acute and five obtuse isosceles triangles. In all of them, the ratio of the longer side to the shorter side is φ. The acute triangles are golden triangles. The obtuse isosceles triangle highlighted via the colored lines in the illustration is a golden gnomon.

The Pentagon, Pentagram and Hippasos

Trigonometric values

See Exact trigonometric constants: Pentagon

As a result, in an isosceles triangle with one or two angles of 36°, the longer of the two side lengths is φ times that of the shorter of the two, both in the case of the acute as in the case of the obtuse triangle.

# ^ "Pentagram" article in The Continuum Encyclopedia of Symbols Becker, Udo, ed., Garmer, Lance W. translator, New York: Continuum Books, 1994, p. 230.

# ^ Signs and Symbols in Christian Art Ferguson, George, Oxford University Press: 1966, p. 59.

# ^ Liungman, Carl G. "Symbol 27:21" in Symbols -- Encyclopedia of Western Signs and Ideograms

# ^ Liungman, Carl G. "Symbol 29:14" in Symbols -- Encyclopedia of Western Signs and Ideograms

# ^ "Pentacle", Oxford English Dictionary.

# ^ Labat, René. Manuel d'épigraphie akkadienne: Signes, Syllabaire, Idéogrammes. The pentagram is symbol number 306 in this system.

# ^ This is a lost book, but its contents are preserved in Damascius, De principiis, quoted in Kirk and Raven, The Pre-Socratic Philosophers, Cambridge Univ. Press, 1956, p. 55.

References

* Grünbaum, B. and G. C. Shephard; Tilings and Patterns, New York: W. H. Freeman & Co., (1987), ISBN 0-7167-1193-1.

* Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993), ed T. Bisztriczky et al, Kluwer Academic (1994) pp. 43-70.

Geometry