.
Routh's theorem
In geometry, Routh's theorem determines the ratio of areas between a given triangle and a triangle formed by the intersection of three cevians. The theorem states that if in triangle ABC points D, E, and F lie on segments BC, CA, and AB, then writing \( \tfrac{CD}{BD} = x, \tfrac{AE}{CE} = y \), and \tfrac{BF}{AF} = z, the signed area of the triangle formed by the cevians AD, BE, and CF is the area of triangle ABC times
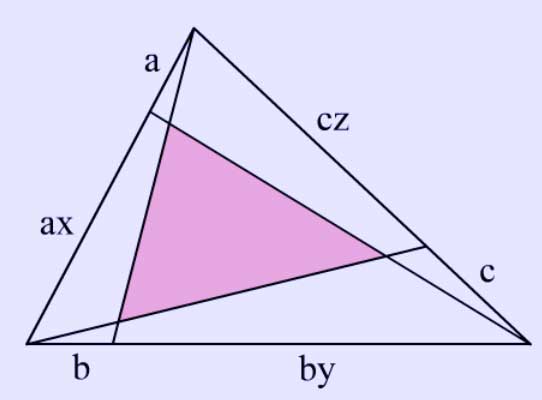
\( \frac{(xyz - 1)^2}{(xy + y + 1)(yz + z + 1)(zx + x + 1)}. \)
This theorem was given by Edward John Routh on page 82 of his Treatise on Analytical Statics with Numerous Examples in 1896. The particular case x = y = z = 2 has become popularized as the one-seventh area triangle. The x = y = z = 1 case implies that the three medians are concurrent (through the centroid).
Proof
Suppose the area of triangleABC is 1. For triangleABD and lineFRC using Menelaus's theorem, We could obtain:
\( \frac{AF}{FB} \times \frac{BC}{CD} \times \frac{DR}{RA} = 1 \)
Then \( \frac{DR}{RA} = \frac{BF}{FA} \frac{DC}{CB} = \frac{zx}{x+1} \)
So the area of triangleARC is:
\( S_{ARC} = \frac{AR}{AD} S_{ADC} = \frac{AR}{AD} \frac{DC}{BC} S_{ABC} = \frac{x}{zx+x+1} \)
Similarly, we could know: \( S_{BPA} = \frac{y}{xy+y+1} \) and \( S_{CQB} = \frac{z}{yz+z+1} \)
Thus the area of trainglePQR is:
\( \displaystyle S_{PQR} = S_{ABC} - S_{ARC} - S_{BPA} - S_{CQB}
= 1 - \frac{x}{zx+x+1} - \frac{y}{xy+y+1} - \frac{z}{yz+z+1}
=\frac{(xyz - 1)^2}{(xz + x + 1)(yx + y + 1)(zy + z + 1)}. \)
References
Murray S. Klamkin and A. Liu (1981) "Three more proofs of Routh's theorem", Crux Mathematicorum 7:199–203.
H. S. M. Coxeter (1969) Introduction to Geometry, statement p. 211, proof pp. 219–20, 2nd edition, Wiley, New York.
J. S. Kline and D. Velleman (1995) "Yet another proof of Routh's theorem" (1995) Crux Mathematicorum 21:37–40
Routh's Theorem, Jay Warendorff, The Wolfram Demonstrations Project.
Weisstein, Eric W., "Routh's Theorem" from MathWorld.
Routh's Theorem by Cross Products at MathPages
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

