Square
A square The sides of a square and its diagonals meet at right angles.
Edges and vertices	4
Schläfli symbols	{4} {}x{}
Coxeter–Dynkin diagrams
Symmetry group	Dihedral (D4)
Area (with t=edge length)	t2
Internal angle (degrees)	90°

In plane (Euclidean) geometry, a square is a regular polygon with four sides.

Classification

A square (regular quadrilateral) is a special case of a rectangle as it has four right angles and parallel sides. Likewise it is also a special case of a rhombus, kite, parallelogram, and trapezoid.

The perimeter of a square whose sides have length t is

P = 4t.

And the area is

A = t².

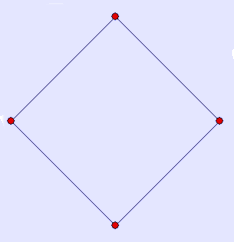
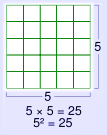
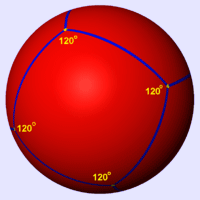
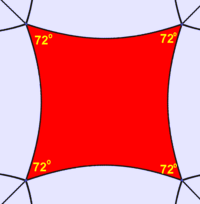
The area of a square is the product of the length of its sides.

In classical times, the second power was described in terms of the area of a square, as in the above formula. This led to the use of the term square to mean raising to the second power.

Standard coordinates

The coordinates for the vertices of a square centered at the origin and with side length 2 are (±1, ±1), while the interior of the same consists of all points (x₀, x₁) with −1 < x_i < 1.

Properties

Each angle in a square is equal to 90 degrees, or a right angle.

The diagonals of a square are equal. Conversely, if the diagonals of a rhombus are equal, then that rhombus must be a square. The diagonals of a square are (about 1.41) times the length of a side of the square. This value, known as Pythagoras’ constant, was the first number proven to be irrational.

If a figure is both a rectangle (right angles) and a rhombus (equal edge lengths) then it is a square.

Other facts

* If a circle is circumscribed around a square, the area of the circle is π / 2 (about 1.57) times the area of the square.

* If a circle is inscribed in the square, the area of the circle is π / 4 (about 0.79) times the area of the square.

* A square has a larger area than any other quadrilateral with the same perimeter ([1]).

* A square tiling is one of three regular tilings of the plane (the others are the equilateral triangle and the regular hexagon).

* The square is in two families of polytopes in two dimensions: hypercube and the cross polytope. The Schläfli symbol for the square is {4}.

* The square is a highly symmetric object. There are four lines of reflectional symmetry and it has rotational symmetry through 90°, 180° and 270°. Its symmetry group is the dihedral group D4.

Non-Euclidean geometry

In non-euclidean geometry, squares are more generally polygons with 4 equal sides and equal angles.

In spherical geometry, a square is a polygon whose edges are great circle arcs of equal distance, which meet at equal angles. Unlike the square of plane geometry, the angles of such a square are larger than a right angle.

In hyperbolic geometry, squares with right angles do not exist. Rather, squares in hyperbolic geometry have angles of less than right angles. Larger squares have smaller angles.

Examples:

Six squares can tile the sphere with 3 squares around each vertex and 120 degree internal angles. This is called a spherical cube. The Schläfli symbol is {4,3}.

Squares can tile the Euclidean plane with 4 around each vertex, with each square having an internal angle of 90 degrees. The Schläfli symbol is {4,4}.

Squares can tile the hyperbolic plane with 5 around each vertex, with each square having 72 degree internal angles. The Schläfli symbol is {4,5}.

See also

* Cube

* Pythagorean theorem

* Square lattice

* Unit square

Links

* Square Calculation

* Animated course (Construction, Circumference, Area)

* Eric W. Weisstein, Square at MathWorld.

* Definiton and properties of a square With interactive applet

Geometry