Symmedian point:

In geometry, three special lines are associated with every triangle, the triangle's symmedians. To construct one, start with a median of the triangle (a line connecting one vertex with the midpoint of the opposite side) then reflect it over the corresponding angle bisector (the line through the same vertex that divides the angle of the triangle there in two equal parts). The resulting line is a symmedian. The three symmedians intersect in a single point, the triangle's symmedian point or Lemoine point.

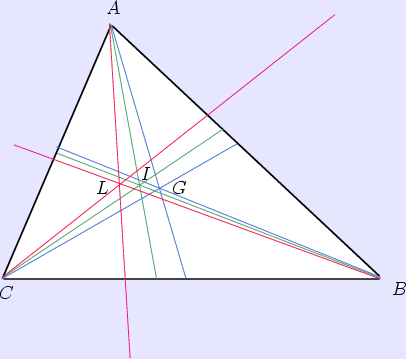
A triangle with medians (blue), angle bisectors (green) and symmedians (red). The symmedians intersect in the Lemoine point L.

The symmedian point of a triangle with sides a, b and c has homogeneous trilinear coordinates [a : b : c].

The symmedian point L can also be constructed differently: the three lines joining the midpoint of a side to the midpoint of the altitude on that side intersect in L. The symmedian point of a right triangle is therefore the midpoint of the altitude on the hypotenuse.

The Gergonne point of a triangle is the same as the symmedian point of the triangle's contact triangle.

The symmedian point is the isogonal conjugate of the triangle's centroid.

References

* Ross Honsberger, "The Symmedian Point," Chapter 7 in Episodes in Nineteenth and Twentieth Century Euclidean Geometry, The Mathematical Association of America, Washington, D.C., 1995.

Lemoine hexagon

Links

* Symmedian and Antiparallel at cut-the-knot

* Symmedian and 2 Antiparallels at cut-the-knot

* Symmedian and the Tangents at cut-the-knot

* An interactive Java applet for the symmedian point

Geometry