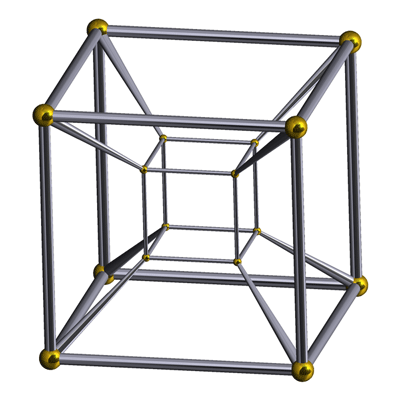
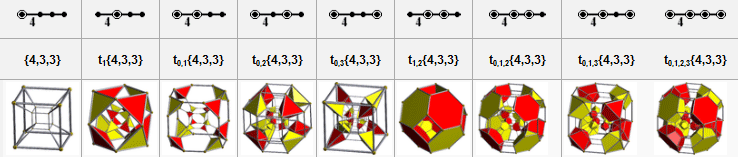
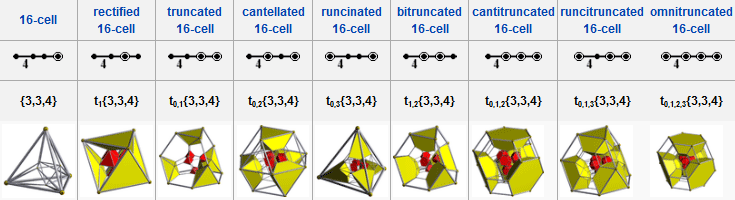
Tesseract

Tesseract, Schlegel diagram

In geometry, the tesseract, also called an 8-cell or regular octachoron, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8 cubical cells. The tesseract is one of the six convex regular 4-polytopes.

A generalization of the cube to dimensions greater than three is called a "hypercube", "n-cube" or "measure polytope". The tesseract is the four-dimensional hypercube, or 4-cube.

According to the Oxford English Dictionary, the word tesseract was coined and first used in 1888 by Charles Howard Hinton in his book A New Era of Thought, from the Greek “τέσσερεις ακτίνες” (“four rays”), referring to the four lines from each vertex to other vertices. Some people have called the same figure a tetracube, and also simply a hypercube (although the term hypercube is also used with dimensions greater than 4).

Geometry

The tesseract can be constructed in a number of ways. As a regular polytope with three cubes folded together around every edge, it has Schläfli symbol {4,3,3}. Constructed as a 4D hyperprism made of two parallel cubes, it can be named as a composite Schläfli symbol {4,3} × { }. As a duoprism, a Cartesian product of two squares, it can be named by a composite Schläfli symbol {4}×{4}.

Since each vertex of a tesseract is adjacent to four edges, the vertex figure of the tesseract is a regular tetrahedron. The dual polytope of the tesseract is called the hexadecachoron, or 16-cell, with Schläfli symbol {3,3,4}.

The standard tesseract in Euclidean 4-space is given as the convex hull of the points (±1, ±1, ±1, ±1). That is, it consists of the points:

A tesseract is bounded by eight hyperplanes (xi = ±1). Each pair of non-parallel hyperplanes intersects to form 24 square faces in a tesseract. Three cubes and three squares intersect at each edge. There are four cubes, six squares, and four edges meeting at every vertex. All in all, it consists of 8 cubes, 24 squares, 32 edges, and 16 vertices.

Projections to 2 dimensions

The construction of a hypercube can be imagined the following way:

* 1-dimensional: Two points A and B can be connected to a line, giving a new line segment AB.
* 2-dimensional: Two parallel line segments AB and CD can be connected to become a square, with the corners marked as ABCD.
* 3-dimensional: Two parallel squares ABCD and EFGH can be connected to become a cube, with the corners marked as ABCDEFGH.
* 4-dimensional: Two parallel cubes ABCDEFGH and IJKLMNOP can be connected to become a hypercube, with the corners marked as ABCDEFGHIJKLMNOP.

This structure is not easily imagined but it is possible to project tesseracts into three- or two-dimensional spaces. Furthermore, projections on the 2D-plane become more instructive by rearranging the positions of the projected vertices. In this fashion, one can obtain pictures that no longer reflect the spatial relationships within the tesseract, but which illustrate the connection structure of the vertices, such as in the following examples:
A diagram showing how to create a tesseract from a point

A tesseract is in principle obtained by combining two cubes. The scheme is similar to the construction of a cube from two squares: juxtapose two copies of the lower dimensional cube and connect the corresponding vertices. Each edge of a tesseract is of the same length. The vertices of the tesseract with respect to the distance along the edges, with respect to the bottom point. This view is of interest when using tesseracts as the basis for a network topology to link multiple processors in parallel computing: the distance between two nodes is at most 4 and there are many different paths to allow weight balancing.

Tesseracts are also bipartite graphs, just as a path, square, cube and tree are.

Projections to 3 dimensions
The rhombic dodecahedron forms the convex hull of the tesseracts vertex-first shadow. The number of vertices in the layers of this projection is 1 4 6 4 1 - the fourth row in Pascal's triangle.
Projection envelopes of the tesseract (each cell is drawn with different color faces, inverted cells are undrawn)

The cell-first parallel projection of the tesseract into 3-dimensional space has a cubical envelope. The nearest and farthest cells are projected onto the cube, and the remaining 6 cells are projected onto the 6 square faces of the cube.

The face-first parallel projection of the tesseract into 3-dimensional space has a cuboidal envelope. Two pairs of cells project to the upper and lower halves of this envelope, and the 4 remaining cells project to the side faces.

The edge-first parallel projection of the tesseract into 3-dimensional space has an envelope in the shape of a hexagonal prism. Six cells project onto rhombic prisms, which are laid out in the hexagonal prism in a way analogous to how the faces of the 3D cube project onto 6 rhombs in a hexagonal envelope under vertex-first projection. The two remaining cells project onto the prism bases.

The vertex-first parallel projection of the tesseract into 3-dimensional space has a rhombic dodecahedral envelope. There are exactly two ways of decomposing a rhombic dodecahedron into 4 congruent parallelepipeds, giving a total of 8 possible parallelepipeds. The images of the tesseract's cells under this projection are precisely these 8 parallelepipeds. This projection is also the one with maximal volume.

Net

The tesseract can be unfolded into eight cubes, just as the cube can be unfolded into six squares (view animation). An unfolding of a polytope is called a net. There are 261 distinct nets of the tesseract.[1] The unfoldings of the tesseract can be counted by mapping the nets to paired trees (a tree together with a perfect matching in its complement).

Image gallery

Perspective projections

Perspective with hidden volume elimination. The red corner is the nearest in 4D and has 4 cubical cells meeting round it.

Stereographic projection

Literature and art

Artists and writers have used the geometry of the tesseract to produce surrealistic effects, for instance in Salvador Dalí's Crucifixion (Corpus Hypercubus), and Robert A. Heinlein's classic science fiction short story "—And He Built a Crooked House—" (1940) in which an earthquake causes a house built in the shape of the net of a tesseract to fold into an actual tesseract.

In the film Flatland: The Movie a model of a tesseract at the end is used to imply the existence of a physical fourth dimension to the inhabitants of the third.

Greg Bear's short science fiction story "Tangents" involves multidimensional visualization and suggests circumstances in which 4-dimensional objects pass through our 3-space.

Madeleine L'Engle in the science fiction-fantasy novel A Wrinkle In Time uses a tesseract as a way of traveling. The easiest way to understand how a tesseract would help with travel is by analogy. Imagine a two dimensional creature, stuck on the surface of a three dimensional cube. Traveling across the surface of the cube would take more time than cutting through the center of the cube, as a three dimensional creature might. Traveling by "tesser" or "wrinkling" allows the children of the book to be transported to places unreachable by normal means of travel.

A tesseract is the basis of the movie Cube 2: Hypercube in which a group of people have to attempt to escape from one.

Others, however, have used the word as a shorthand for something strange or unknown without any reference to the actual figure, as in Alex Garland's novel The Tesseract.

Related uniform polytopes

Name	tesseract	rectified tesseract	truncated tesseract	cantellated tesseract	runcinated tesseract	bitruncated tesseract	cantitruncated tesseract	runcitruncated tesseract	omnitruncated tesseract
Coxeter-Dynkin diagram
Schläfli symbol
Schlegel diagram

Name	16-cell	rectified 16-cell	truncated 16-cell	cantellated 16-cell	runcinated 16-cell	bitruncated 16-cell	cantitruncated 16-cell	runcitruncated 16-cell	omnitruncated 16-cell
Coxeter-Dynkin diagram
Schläfli symbol
Schlegel diagram