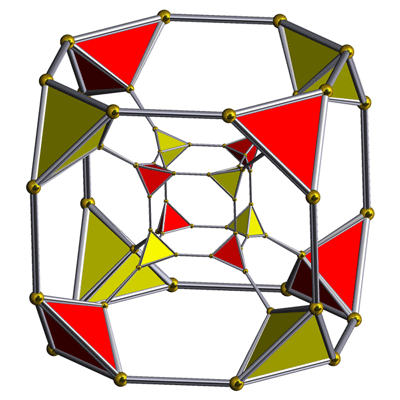
Truncated tesseract, Schlegel diagram
(tetrahedron cells visible)
In geometry, a truncated tesseract is a uniform polychoron (4-dimensional uniform polytope) which is bounded by 24 cells: 8 truncated cubes, and 16 tetrahedra.
Construction
The truncated tesseract may be constructed by truncating the vertices of the tesseract at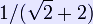 
of the edge length. A regular tetrahedron is formed at each truncated vertex.
The Cartesian coordinates of the vertices of a truncated tesseract having edge length 2 is given by all permutations of:
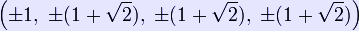
Projections
A stereoscopic 3D projection of a truncated tesseract.
In the truncated cube first parallel projection of the truncated tesseract into 3-dimensional space, the image is laid out as follows:
* The projection envelope is a cube.
* Two of the truncated cube cells project onto a truncated cube inscribed in the cubical envelope.
* The other 6 truncated cubes project onto the square faces of the envelope.
* The 8 tetrahedral volumes between the envelope and the triangular faces of the central truncated cube are the images of the 16 tetrahedra, a pair of cells to each image.
Related uniform polytopes
| Name |
tesseract |
rectified
tesseract |
truncated
tesseract |
cantellated
tesseract |
runcinated
tesseract |
bitruncated
tesseract |
cantitruncated
tesseract |
runcitruncated
tesseract |
omnitruncated
tesseract |
Coxeter-Dynkin
diagram |
 |
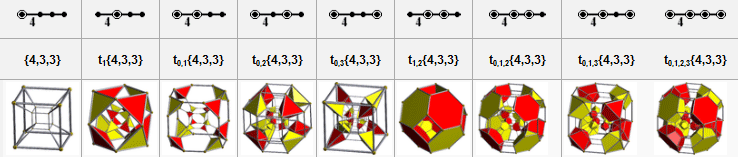Schläfli
symbol |
Schlegel
diagram |
| |
| Name |
16-cell |
rectified
16-cell |
truncated
16-cell |
cantellated
16-cell |
runcinated
16-cell |
bitruncated
16-cell |
cantitruncated
16-cell |
runcitruncated
16-cell |
omnitruncated
16-cell |
Coxeter-Dynkin
diagram |
 |
Schläfli
symbol |
Schlegel
diagram |
Images: Robert Webb's Great Stella software
