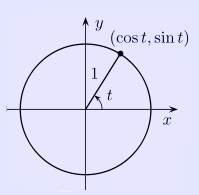
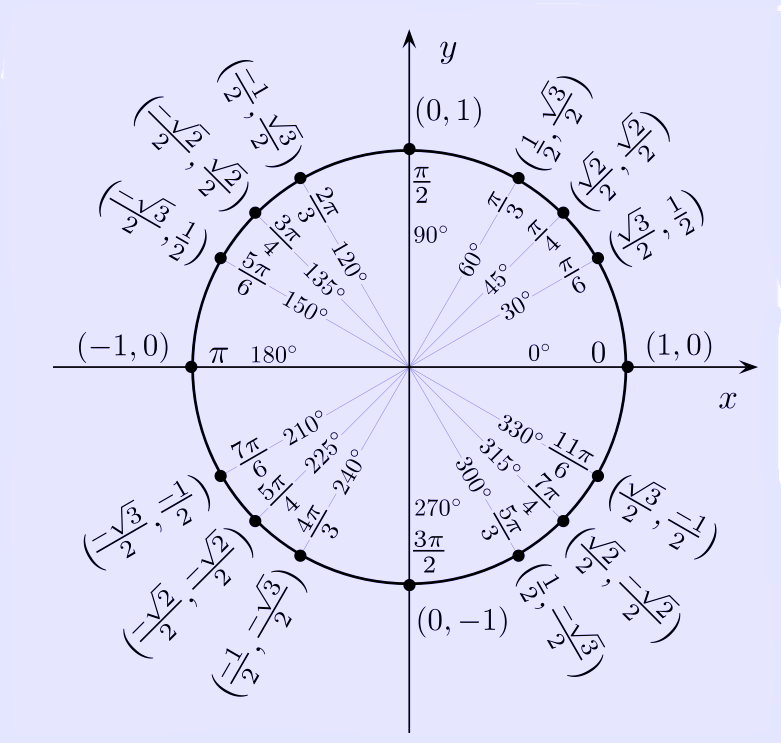
In mathematics, a unit circle is a circle with a unit radius, i.e., a circle whose radius is 1. Frequently, especially in trigonometry, "the" unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Euclidean plane. The unit circle is often denoted S¹; the generalization to higher dimensions is the unit sphere.

If (x, y) is a point on the unit circle in the first quadrant, then x and y are the lengths of the legs of a right triangle whose hypotenuse has length 1. Thus, by the Pythagorean theorem, x and y satisfy the equation

x² + y² = 1.

Since x² = (−x)² for all x, and since the reflection of any point on the unit circle about the x- or y-axis is also on the unit circle, the above equation holds for all points (x, y) on the unit circle, not just those in the first quadrant.

One may also use other notions of "distance" to define other "unit circles;" see the article on mathematical norms for examples.

Trigonometric functions on the unit circle

The trigonometric functions cosine and sine may be defined on the unit circle as follows. If (x, y) is a point of the unit circle, and if the ray from the origin (0, 0) to (x, y) makes an angle t from the positive x-axis, (where counterclockwise turning is positive), then

The equation x² + y² = 1 gives the relation

Note that cos²(t)=(cos(t))². This is the standard shorthand for expressing powers of trigonometric functions.

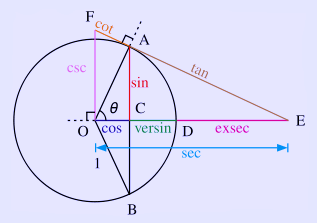
All of the trigonometric functions of the angle θ can be constructed geometrically in terms of a unit circle centered at O.

The unit circle also gives an intuitive way of realizing that sine and cosine are periodic functions, with the identities

for any integer k.

These identities come from the fact that the x- and y-coordinates of a point on the unit circle remain the same after the angle t is increased or decreased by any number of revolutions (1 revolution = 2π radians).

When working with right triangles, sine, cosine, and other trigonometric functions only make sense for angle measures more than zero and less than π/2. However, using the unit circle, these functions have sensible, intuitive meanings for any real-valued angle measure.

In fact, not only sine and cosine, but all of the six standard trigonometric functions — sine, cosine, tangent, cotangent, secant, and cosecant, as well as archaic functions like versine and exsecant — can be defined geometrically in terms of a unit circle, as shown at right.

Circle group

Complex numbers can be identified with points in the Euclidean plane, namely the number a + bi is identified with the point (a, b). Under this identification, the unit circle is a group under multiplication, called the circle group. This group has important applications in mathematics and science.

See also

* Angle measure
* Unit sphere
* Unit square
* Unit disc
* Circle group

Links

* Eric W. Weisstein, Unit circle at MathWorld.

* An excellent Flash animation for learning the unit circle

* Printable, full page, unit circle handout

Geometry