.

In the mathematical field of graph theory, an antiprism graph is a graph that has one of the antiprisms as its skeleton. An n-sided antiprism has 2n vertices and 4n edges. They are regular, polyhedral (and therefore by necessity also 3-vertex-connected, vertex-transitive, and planar graphs), and also Hamiltonian graphs.[1]

An antiprism graph is a special case of a circulant graph, Ci_2n(2,1).

Octahedral graph – 6 vertices, 12 edges
square antiprismatic graph – 8 vertices, 16 edges
Pentagonal antiprismatic graph – 10 vertices, 20 edges
Hexagonal antiprismatic graph – 12 vertices, 24 edges
Heptagonal antiprismatic graph – 14 vertices, 28 edges
Octagonal antiprismatic graph – 16 vertices, 32 edges
...

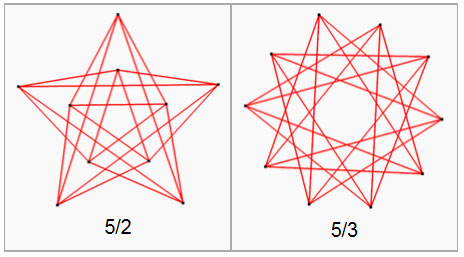
There are also related star polygon antiprisms:

Pentagrammic antiprismatic graph – 10 vertices, 20 edges
Pentagrammic crossed-antiprismatic graph – 10 vertices, 20 edges
...

.

Antiprism graph